
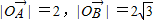 ,∠AOB=90°,单位圆O与OA交于C,
,∠AOB=90°,单位圆O与OA交于C, ,P为单位圆O上的动点.
,P为单位圆O上的动点. ,求λ的值;
,求λ的值; 的最小值为f(λ),求f(λ)的表达式及f(λ)的最小值.
的最小值为f(λ),求f(λ)的表达式及f(λ)的最小值.
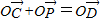 得
得 ,从而可求
,从而可求 =(2-2λ-cosα,2
=(2-2λ-cosα,2 λ-sinα)可得f(λ)=
λ-sinα)可得f(λ)= ,结合二次函数的性质可求
,结合二次函数的性质可求 ≥
≥ 当且仅当P在线段OD上等号成立可得f(λ)=
当且仅当P在线段OD上等号成立可得f(λ)= 下同法一
下同法一 解:(1)以O为原点,OA为x轴,OB为y轴建立直角坐标系
解:(1)以O为原点,OA为x轴,OB为y轴建立直角坐标系 ),C(1,0)
),C(1,0) 由O
由O
 16λ2-4λ=0⇒λ=0或λ=
16λ2-4λ=0⇒λ=0或λ= (5分)
(5分) =(2-2λ-cosα,2
=(2-2λ-cosα,2 λ-sinα)
λ-sinα) ≥16λ2-8λ+5-
≥16λ2-8λ+5-
 -1(4分)
-1(4分) )2+3≥3
)2+3≥3 )=
)= -1(2分)
-1(2分) ≥
≥ 当且仅当P在线段OD上等号成立
当且仅当P在线段OD上等号成立 (4分)
(4分) )2+3≥3
)2+3≥3 )=
)= -1(2分)
-1(2分)

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
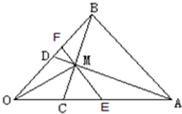 如图,在△OAB中,
如图,在△OAB中,| OC |
| 1 |
| 3 |
| OA |
| OD |
| 1 |
| 2 |
| OB |
| OA |
| a |
| OB |
| b |
| a |
| b |
| OM |
| OE |
| OA |
| OF |
| OB |
| 1 |
| λ |
| 2 |
| μ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•杭州二模)如图,在△OAB中,C为OA上的一点,且
(2013•杭州二模)如图,在△OAB中,C为OA上的一点,且| OC |
| 2 |
| 3 |
| OA |
| OP |
| OB |
| OC |
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在△OAB中,已知|O
如图,在△OAB中,已知|O| A |
| B |
| 3 |
| D |
| B |
| C |
| P |
| D |
| D |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=
如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=| 1 |
| 3 |
| OA |
| a |
| OB |
| b |
| a |
| b |
| OC |
| DC |
| DE |
查看答案和解析>>
科目:高中数学 来源: 题型:
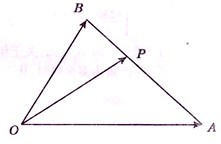 如图,在△OAB中,已知P为线段AB上的一点,且|
如图,在△OAB中,已知P为线段AB上的一点,且|| AP |
| PB |
| OA |
| OB |
| OP |
| OA |
| |OB| |
| OP |
| AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com