
分析 (Ⅰ)通过讨论x的范围,求出不等式的解集,取并集即可;(Ⅱ)根据绝对值的性质求出f(x)+3|x-2|的最小值,从而求出m的范围即可.
解答 解:(Ⅰ)f(x)=|x+1|-|2x-4|=|x+1|-2|x-2|≥1,
x≥2时,x+1-2x+4≥1,解得:x≤4,
-1<x<2时,x+1+2x-4≥1,解得:x≥$\frac{4}{3}$,
x≤-1时,-x-1+2x-4≥1,无解,
故不等式的解集是[$\frac{4}{3}$,4];
(Ⅱ)若对?x∈R,都有f(x)+3|x-2|>m,
即若对?x∈R,都有|x+1|+|x-2|>m,
而|x+1|+|x-2|≥|x+1-x+2|=3,
故m<3.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
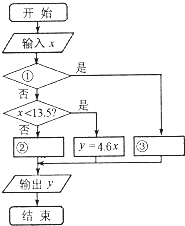 为了鼓励市民节约用水,太原市对已实施“一户一表、水表出户”的居民生活用水的收费标准规定如下:一级水量每户每月9立方米及以下,每立方米销售价格为2.30元;二级水量每户每月9立方米以上至13.5立方米,每立方米销售价格为4.60元;三级水量每户每月13.5立方米及以上,每立方米销售价格为6.90元,如图是按上述规定计算太原市居民每户每月生活用水费用的程序框图,但步骤没有全部给出,请将其补充完整(将答案写在下列横线上).①x≤9?;②y=6.9x;③y=2.3x.
为了鼓励市民节约用水,太原市对已实施“一户一表、水表出户”的居民生活用水的收费标准规定如下:一级水量每户每月9立方米及以下,每立方米销售价格为2.30元;二级水量每户每月9立方米以上至13.5立方米,每立方米销售价格为4.60元;三级水量每户每月13.5立方米及以上,每立方米销售价格为6.90元,如图是按上述规定计算太原市居民每户每月生活用水费用的程序框图,但步骤没有全部给出,请将其补充完整(将答案写在下列横线上).①x≤9?;②y=6.9x;③y=2.3x.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2i | B. | 1+2i | C. | -1-2i | D. | -1+2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
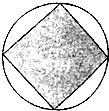 我们知道,可以用模拟的方法估计圆周率p的近似值,如图,在圆内随机撒一把豆子,统计落在其内接正方形中的豆子数目,若豆子总数为n,落到正方形内的豆子数为m,则圆周率p的估算值是( )
我们知道,可以用模拟的方法估计圆周率p的近似值,如图,在圆内随机撒一把豆子,统计落在其内接正方形中的豆子数目,若豆子总数为n,落到正方形内的豆子数为m,则圆周率p的估算值是( )| A. | $\frac{n}{m}$ | B. | $\frac{2n}{m}$ | C. | $\frac{3n}{m}$ | D. | $\frac{2m}{n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com