
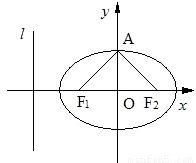
 如图,椭圆C:
如图,椭圆C: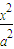 +
+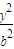 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,点(
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,点( ,
, )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.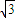 ,
,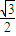 )代入即可求得λ,则椭圆的方程可得.
)代入即可求得λ,则椭圆的方程可得. PQ推断出PF1+F1Q=PQ,与“三角形两边之和大于第三边”矛盾,假设不成立,再看若F1Q=PQ,设出P点坐标,则Q点坐标可得,进而表示出F1Q和PQ求得x和y的关系,与椭圆方程联立求得P点坐标.判断出存在点P(-
PQ推断出PF1+F1Q=PQ,与“三角形两边之和大于第三边”矛盾,假设不成立,再看若F1Q=PQ,设出P点坐标,则Q点坐标可得,进而表示出F1Q和PQ求得x和y的关系,与椭圆方程联立求得P点坐标.判断出存在点P(- ,±
,± ),使得△PF1Q为等腰三角
),使得△PF1Q为等腰三角 +
+ =1(a>b>0),
=1(a>b>0), =
=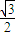 ,
,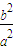 =
= .
. +
+ =λ.
=λ. ,
,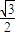 ),解得λ=1,
),解得λ=1,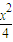 +
+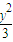 =1.
=1.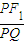 =e=
=e= ,得PF1=
,得PF1= PQ.所以PF1≠PQ.
PQ.所以PF1≠PQ. PQ,∴PF1+F1Q=PQ,
PQ,∴PF1+F1Q=PQ, =4+x,
=4+x,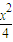 +
+ =1,得y2=3-
=1,得y2=3- x2.
x2. x2=16+8x+x2,
x2=16+8x+x2, x2+8x+4=0.
x2+8x+4=0. 或x=-4.
或x=-4. .所以P(-
.所以P(- ,±
,± ).
). ,±
,±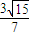 ),使得△PF1Q为等腰三角
),使得△PF1Q为等腰三角

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
 如图,椭圆C:
如图,椭圆C: +
+ =1(a>b>0)的左右顶点为A1,A2,左右焦点为F1,F2,其中F1,F2是A1A2的三等分点,A是椭圆上任意一点,且|AF1|+|AF2|=6.
=1(a>b>0)的左右顶点为A1,A2,左右焦点为F1,F2,其中F1,F2是A1A2的三等分点,A是椭圆上任意一点,且|AF1|+|AF2|=6.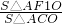 ,n=
,n=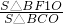 ,若点A在第一象限,求m+n的取值范围.
,若点A在第一象限,求m+n的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省常州高级中学高三(上)12月月考数学试卷(理科)(解析版) 题型:解答题
 +
+ =1的右顶点是A,上下两个顶点分别为B,D,四边形DAMB是矩形(O为坐标原点),点E,P分别是线段OA,MA的中点.
=1的右顶点是A,上下两个顶点分别为B,D,四边形DAMB是矩形(O为坐标原点),点E,P分别是线段OA,MA的中点. 求证:直线SR过定点,并求出此定点的坐标.
求证:直线SR过定点,并求出此定点的坐标.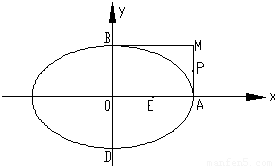
查看答案和解析>>
科目:高中数学 来源:2009-2010学年数学暑期综合练习(2)(解析版) 题型:解答题
 如图,椭圆C:
如图,椭圆C: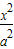 +
+ =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,点(
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,点( ,
,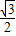 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.查看答案和解析>>
科目:高中数学 来源:2011年重庆市高考数学二模试卷(文科)(解析版) 题型:解答题
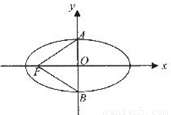
 =1(a>b>0)的左焦点为
=1(a>b>0)的左焦点为 ,上下顶点分别为A,B,已知△AFB是等边三角形.
,上下顶点分别为A,B,已知△AFB是等边三角形.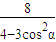 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com