
分析 (1)利用函数单调性求解,
(2)根据二次函数在闭区间上的最值求解
(3)换元转化为二次函数,注意新元的范围
(4)变形y=2(x-1)-$\sqrt{x-1}$+2利用换元法求解
(5)分离参数转化为反比例函数值域求解.
解答 解:(1)y=$\sqrt{{x}^{2}+5}$;
∵x2≥0,
∴x2+5≥5,
即y$≥\sqrt{5}$
值域为:[$\sqrt{5}$,+∞)
(2)y=x2-4x+6,1≤x<5;
对称轴为:x=2,y小=22-2×4+6=2
利用二次函数的对称性得出:y大=52-4×5+6=11
值域为:[2,11]
(3)y=-x4+x2$+\frac{1}{4}$,x∈R,
设t=x2,t≥0
y=t2+t$+\frac{1}{4}$,x∈R
根据二次函数的性质得出:最小值为$\frac{1}{4}$
故值域为;[$\frac{1}{4}$,+∞)
(4)y=2x-$\sqrt{x-1}$=2(x-1)-$\sqrt{x-1}$+2
设t=$\sqrt{x-1}$≥0,
y=2t2-t+2.
根据二次函数的性质得出:对称轴x=$\frac{1}{4}$
最小值为:2×$\frac{1}{16}$$-\frac{1}{4}$+2=$\frac{15}{8}$,
故值域为:[$\frac{15}{8}$,+∞)
(5)y=$\frac{2x+1}{3x+5}$=$\frac{2}{3}$$-\frac{7}{3x+5}$
根据反比例函数的性质得出:
y=$\frac{7}{3x+5}$值域为:(-∞,0)∪(0+∞)
y=$\frac{2}{3}$$-\frac{7}{3x+5}$值域为:(-∞,$\frac{2}{3}$)∪($\frac{2}{3}$+∞)
故值域为:(-∞,$\frac{2}{3}$)∪($\frac{2}{3}$+∞)
点评 本题综合考察了常见函数的值域的求解方法,换元法,二次函数等求解,难度不大,属于中档题,熟练掌握函数性质最重要.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
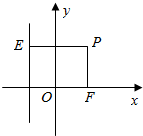 如图,点O是坐标原点,点F(p,0),其中p>0,点E在直线l:x=-p上,点F到直线x+y=0的距离等于$\sqrt{2}$,动点p满足|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|,$\overrightarrow{EP}$=λ$\overrightarrow{OF}$(λ∈R,且λ≠0).
如图,点O是坐标原点,点F(p,0),其中p>0,点E在直线l:x=-p上,点F到直线x+y=0的距离等于$\sqrt{2}$,动点p满足|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|,$\overrightarrow{EP}$=λ$\overrightarrow{OF}$(λ∈R,且λ≠0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com