练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-11,已知在△ABC中,AB =AC,以AB为直径的⊙O交BC于D,过D点作⊙O的切线交AC于E.

    图2-11

    求证:（1）DE⊥AC;

    （2）BD2=CE·CA.

    思路分析:本例是考查切线的性质与直径所对的圆周角是直角的综合题,掌握常见的辅助线作法是解题关键,即连结圆心和切点的半径,根据切线的性质,则有半径垂直于这条切线.

    证明:(1)连结OD、AD.?

    ∵DE是⊙O的切线,D为切点,?

    ∴OD⊥DE.?

    ∵AB是⊙O的直径,?

    ∴AD⊥BC.∴AB =AC,BD =DC.?

    ∴OD∥AC,DE⊥AC.?

    (2)∵AD⊥BC,DE⊥AC,?

    ∴△CDE∽△CAD.?

    ∴=.∴CD2 =CE·CA.?

    ∴BD =DC.∴BD2 =CE·CA.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年广东省深圳市高三2月调研考试理科数学试卷（解析版） 题型：解答题

    某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况，随机抽查了该市当天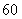名网友的网购金额情况，得到如下数据统计表（如图）：

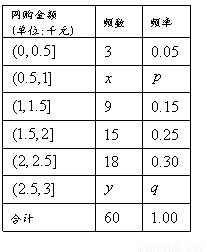
    若网购金额超过千元的顾客定义为“网购达人”，网购金额不超过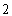千元的顾客定义为“非网购达人”，已知“非网购达人”与“网购达人”人数比恰好为．

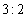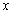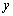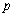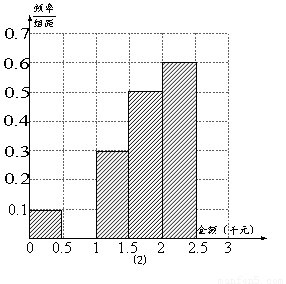
    （1）试确定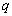，，，的值，并补全频率分布直方图（如图(2)）．

    （2）该营销部门为了进一步了解这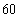名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定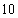人，若需从这人中随机选取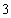人进行问卷调查．设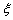为选取的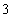人中“网购达人”的人数，求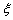的分布列和数学期望．

     

    查看答案和解析>>

    科目：高中数学 来源：2013届吉林省高二上学期质量检测理科数学 题型：填空题

    .“沃尔玛”商场在国庆“62”黄金周的促销活动中,对

    10月2日9时至14时的销售额进行统计,其频率分布

    直方图如右下图所示.已知9时至10时的销售额为

    2.5万元,则11时至12时的销售额为________万元.

     

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

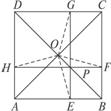
    如图2-2-11，已知P为正方形ABCD的对角线BD上的一点，通过P作正方形的边的垂线，垂足为E、F、G、H.你能判断出E、F、G、H是否在同一个圆上吗？试说明你的猜想.

    图2-2-11

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    梯形的两腰和一底如果相等,它的对角线必平分另一底上的两个角.

    已知在梯形ABCD中(如图2-1-11),AB=DC=AD,AC和BD是它的对角线,求证:AC平分∠BCD,DB平分∠CBA.

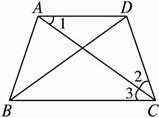
    图2-1-11

    查看答案和解析>>

    同步练习册答案