练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)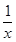＝－lnx在区间(1,2)内有一个零点x0，若用二分法求x0的近似值(精确度0.1)，则需要将区间等分的次数为(　　)

    A．3                                B．4

    C．5                                D．6

     

    【答案】

    B

    【解析】由求解方程近似解的步骤可知需将区间等分4次．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：蚌埠二中2007届高三第一学期期中考试数学试题 题型：044

    解答题

    (理)已知f(x)＝ln(ex＋a)(a＞0)(1)求y＝f(x)的反函数及f(x)的导函数．(2)假设x∈[ln3a，ln4a]，不等式：|m－f－1(x)|＋lnf′(x)＜0恒成立求m范围．

    查看答案和解析>>

    科目：高中数学 来源：江西省九江一中2012届高三上学期第三次月考数学文科试题 题型：013

    已知f(x)＝ln(x2＋1)，g(x)＝()x－m，若任意x1∈[0，3]，存在x2∈[1，2]，使得f(x1)≥g(x2)，则实数m的取值范围是

    [　　]
    A．

    [，＋∞)

    B．

    (－∞，]

    C．

    [，＋∞)

    D．

    (－∞，]

    查看答案和解析>>

    科目：高中数学 来源：山东肥城六中2008届高中数学(新课标)模拟示范卷4 题型：044

    已知f(x)＝ln(x2＋1)－(ax－2)

    (Ⅰ)若函数f(x)是R上的增函数，求a的取值取值范围；

    (Ⅱ)若|a|＜1，求f(x)的单调增区间．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省高三练习数学 题型：解答题

    已知f (x)＝ax－ln(－x)，x∈(－e,0)，g(x)＝－，其中e是自然常数，a∈R．

    （1）讨论a＝－1时, f (x)的单调性、极值；

    （2）求证：在（1）的条件下，|f (x)|＞g(x)＋1/2；

    （3）是否存在实数a，使f (x)的最小值是3，如果存在，求出a的值；如果不存在，说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f (x)＝ax－ln(－x)，x∈(－e,0)，g(x)＝－，其中e是自然常数，a∈R．
    （1）讨论a＝－1时, f (x)的单调性、极值；
    （2）求证：在（1）的条件下，|f (x)|＞g(x)＋；
    （3）是否存在实数a，使f (x)的最小值是3，如果存在，求出a的值；如果不存在，说明理由．

     

    查看答案和解析>>

    同步练习册答案