
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省武威一中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省武威一中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省高三9月第一次阶段性达标考试理科数学试卷(解析版) 题型:解答题
.(12分)飞机每飞行1小时的费用由两部分组成,固定部分为4900元,变动部分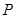 (元)与飞机飞行速度
(元)与飞机飞行速度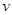 (千米∕小时)的函数关系式是
(千米∕小时)的函数关系式是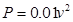 ,已知甲乙两地的距离为
,已知甲乙两地的距离为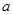 (千米).
(千米).
(1)试写出飞机从甲地飞到乙地的总费用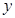 (元)关于速度
(元)关于速度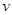 (千米∕小时)的函数关系式;
(千米∕小时)的函数关系式;
(2)当飞机飞行速度为多少时,所需费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com