
【题目】已知抛物线![]() ,抛物线
,抛物线![]() 上横坐标为
上横坐标为![]() 的点到焦点
的点到焦点![]() 的距离为
的距离为![]() .
.
(Ⅰ)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(Ⅱ)过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于不同的两点
于不同的两点![]() ,交直线
,交直线![]() 于点
于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() . 是否存在这样的直线
. 是否存在这样的直线![]() ,使得
,使得![]() ? 若不存在,请说明理由;若存在,求出直线
? 若不存在,请说明理由;若存在,求出直线![]() 的方程.
的方程.
【答案】(Ⅰ) ![]() ,
,![]() . (Ⅱ)存在,
. (Ⅱ)存在,![]() 或
或![]() .
.
【解析】
(I)根据抛物线的定义求得抛物线的标准方程以及准线飞航程.
(II)设出直线![]() 的方程
的方程![]()
![]() ,联立直线的方程和抛物线的方程,消去
,联立直线的方程和抛物线的方程,消去![]() 后根据判别式大于零求得
后根据判别式大于零求得![]() 的取值范围,写出韦达定理.结合
的取值范围,写出韦达定理.结合![]() 得到直线
得到直线![]() 与直线
与直线![]() 的斜率相等(或者转化为
的斜率相等(或者转化为![]() ),由此列方程,解方程求得
),由此列方程,解方程求得![]() 的值,也即求得直线
的值,也即求得直线![]() 的方程.
的方程.
(Ⅰ)因为横坐标为![]() 的点到焦点的距离为
的点到焦点的距离为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以![]()
所以准线方程为![]() .
.
(Ⅱ)显然直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]()
![]() ,
,![]() .
.
联立得 消去
消去![]() 得
得![]() .
.
由![]() ,解得
,解得![]() . 所以
. 所以![]() 且
且![]() .
.
由韦达定理得![]() ,
,![]() .
.
方法一:
直线![]() 的方程为
的方程为![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因为![]() ,所以直线
,所以直线![]() 与直线
与直线![]() 的斜率相等
的斜率相等
又![]() ,所以
,所以 .
.
整理得![]() ,即
,即![]() ,
,
化简得![]() ,
,![]()
![]() ,即
,即![]() .
.
所以![]() ,整理得
,整理得![]() ,
,
解得![]() . 经检验,
. 经检验,![]() 符合题意.
符合题意.
所以存在这样的直线![]() ,直线
,直线![]() 的方程为
的方程为![]() 或
或![]()
方法二:
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
整理得![]() ,即
,即![]() ,
,
整理得![]() .
.
解得![]() ,经检验,
,经检验,![]() 符合题意.
符合题意.
所以存在这样的直线![]() ,直线
,直线![]() 的方程为
的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,椭圆上的点到左焦点的最小值为
,椭圆上的点到左焦点的最小值为![]() .
.
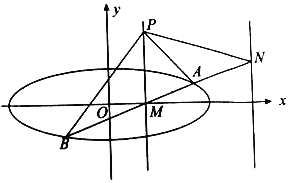
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为直线
为直线![]() 上任意一点,设直线
上任意一点,设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,记
,记![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,则是否存在实数
,则是否存在实数![]() ,使得
,使得![]() 恒成立?若是,请求出
恒成立?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 表示从左到右依次排列的9盏灯,现制定开灯与关灯的规则如下:
表示从左到右依次排列的9盏灯,现制定开灯与关灯的规则如下:
(1)对一盏灯进行开灯或关灯一次叫做一次操作;
(2)灯![]() 在任何情况下都可以进行一次操作;对任意的
在任何情况下都可以进行一次操作;对任意的![]() ,要求灯
,要求灯![]() 的左边有且只有灯
的左边有且只有灯![]() 是开灯状态时才可以对灯
是开灯状态时才可以对灯![]() 进行一次操作.如果所有灯都处于开灯状态,那么要把灯
进行一次操作.如果所有灯都处于开灯状态,那么要把灯![]() 关闭最少需要_____次操作;如果除灯
关闭最少需要_____次操作;如果除灯![]() 外,其余8盏灯都处于开灯状态,那么要使所有灯都开着最少需要_____次操作.
外,其余8盏灯都处于开灯状态,那么要使所有灯都开着最少需要_____次操作.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动.在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,
的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com