
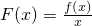 在I上是减函数,则称函数y=f(x)在I上是“慢增函数”.若函数h(x)=x2
在I上是减函数,则称函数y=f(x)在I上是“慢增函数”.若函数h(x)=x2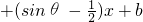 (θ,b是常数)在(0,1]上是“慢增函数”,下面的θ和正数b能满足的条件的是
(θ,b是常数)在(0,1]上是“慢增函数”,下面的θ和正数b能满足的条件的是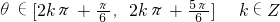
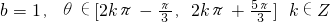
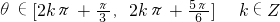
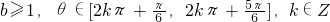
 在(0,1]上单调递减,由此可求出θ及正数b满足的条件.
在(0,1]上单调递减,由此可求出θ及正数b满足的条件. )x+b(θ、b是常数)在(0,1]上是“慢增函数”
)x+b(θ、b是常数)在(0,1]上是“慢增函数” )x+b在(0,1]上是增函数,
)x+b在(0,1]上是增函数, =x+
=x+ +(sinθ-
+(sinθ- )在(0,1]上是减函数,
)在(0,1]上是减函数, )x+b在(0,1]上是增函数,得h′(x)≥0
)x+b在(0,1]上是增函数,得h′(x)≥0 )≥0在(0,1]上恒成立,
)≥0在(0,1]上恒成立, ≤0,
≤0, ,
, ,2kπ+
,2kπ+ ],k∈Z.
],k∈Z. 在(0,1]上是减函数,得F′(x)≤0在(0,1]上恒成立,
在(0,1]上是减函数,得F′(x)≤0在(0,1]上恒成立,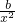 ≤0,b≥x2在(0,1]上恒成立,
≤0,b≥x2在(0,1]上恒成立, ,2kπ+
,2kπ+ ],k∈Z时,h(x)在(0,1]上是“慢增函数”.
],k∈Z时,h(x)在(0,1]上是“慢增函数”.

科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省七市州高三(下)4月联考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com