
ЎҫМвДҝЎҝ2018Дк№ъјКЖ№БӘЧЬҫцИьФЪә«№ъИКҙЁҫЩРРЈ¬ұИИьКұјдОӘ12ФВ13©Ғ12ФВ16ИХЈ¬ФЪДРЧУөҘҙтПоДҝЈ¬ЦР№ъ¶УЧјұёСЎЕЙ4ИЛІОјУ.ТСЦӘ№ъјТТ»ПЯ¶У№І6Гы¶УФұЈ¬¶юПЯ¶У№І4Гы¶УФұ.
ЈЁ1Ј©ЗуЗЎәГУР3Гы№ъјТТ»ПЯ¶У¶УФұІОјУұИИьөДёЕВКЈ»
ЈЁ2Ј©ЙиЛж»ъұдБҝXұнКҫІОјУұИИьөД№ъјТ¶юПЯ¶У¶УФұөДИЛКэЈ¬ЗуXөД·ЦІјБРЈ»
ЈЁ3Ј©ДРЧУөҘҙтҫцИьКЗБЦёЯФ¶ЈЁЦР№ъЈ©¶ФХуХЕұҫЦЗәНЈЁИХұҫЈ©Ј¬ұИИьІЙУГЖЯҫЦЛДКӨЦЖЈ¬ТСЦӘФЪГҝҫЦұИИьЦРЈ¬БЦёЯФ¶»сКӨөДёЕВКОӘ![]() Ј¬ХЕұҫЦЗәН»сКӨөДёЕВКОӘ
Ј¬ХЕұҫЦЗәН»сКӨөДёЕВКОӘ![]() Ј¬З°БҪҫЦұИИьЛ«·ҪёчКӨТ»ҫЦЈ¬ЗТёчҫЦұИИьөДҪб№ыПа»Ҙ¶АБўЈ¬ЗуБЦёЯФ¶»сөГДРЧУөҘҙт№ЪҫьөДёЕВК.
Ј¬З°БҪҫЦұИИьЛ«·ҪёчКӨТ»ҫЦЈ¬ЗТёчҫЦұИИьөДҪб№ыПа»Ҙ¶АБўЈ¬ЗуБЦёЯФ¶»сөГДРЧУөҘҙт№ЪҫьөДёЕВК.
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©·ЦІјБРјыҪвОцЈ»ЈЁ3Ј©
Ј»ЈЁ2Ј©·ЦІјБРјыҪвОцЈ»ЈЁ3Ј©![]()
ЎҫҪвОцЎҝ
ЈЁ1Ј©№ъјТТ»ПЯ¶У№І6Гы¶УФұЈ¬¶юПЯ¶У№І4Гы¶УФұЈ®СЎЕЙ4ИЛІОјУұИИьЈ¬»щұҫКВјюЧЬКэ![]() Ј¬ЗЎәГУР3Гы№ъјТТ»ПЯ¶У¶УФұІОјУұИИь°ьә¬өД»щұҫКВјюёцКэ
Ј¬ЗЎәГУР3Гы№ъјТТ»ПЯ¶У¶УФұІОјУұИИь°ьә¬өД»щұҫКВјюёцКэ![]() Ј¬УЙҙЛДЬЗуіцЗЎәГУР3Гы№ъјТТ»ПЯ¶У¶УФұІОјУұИИьөДёЕВКЈ® ЈЁ2Ј©
Ј¬УЙҙЛДЬЗуіцЗЎәГУР3Гы№ъјТТ»ПЯ¶У¶УФұІОјУұИИьөДёЕВКЈ® ЈЁ2Ј©![]() өДИЎЦөОӘ0Ј¬1Ј¬2Ј¬3Ј¬4Ј¬·ЦұрЗуіцПаУҰөДёЕВКЈ¬УЙҙЛДЬЗуіцXөД·ЦІјБРЈ® ЈЁ3Ј©·ЦұрЗуіц
өДИЎЦөОӘ0Ј¬1Ј¬2Ј¬3Ј¬4Ј¬·ЦұрЗуіцПаУҰөДёЕВКЈ¬УЙҙЛДЬЗуіцXөД·ЦІјБРЈ® ЈЁ3Ј©·ЦұрЗуіц![]() »сКӨЎў
»сКӨЎў![]() »сКӨЎў
»сКӨЎў![]() »сКӨөДёЕВКЈ¬УЙҙЛАыУГ»ҘівКВјюёЕВКјУ·Ё№«КҪДЬЗуіцБЦёЯФ¶»сөГ№ЪҫьөДёЕВКЈ®
»сКӨөДёЕВКЈ¬УЙҙЛАыУГ»ҘівКВјюёЕВКјУ·Ё№«КҪДЬЗуіцБЦёЯФ¶»сөГ№ЪҫьөДёЕВКЈ®
(1)№ъјТТ»ПЯ¶У№І6Гы¶УФұЈ¬¶юПЯ¶У№І4Гы¶УФұ.СЎЕЙ4ИЛІОјУұИИьЈ¬
»щұҫКВјюЧЬКэ![]() Ј¬
Ј¬
ЗЎәГУР3Гы№ъјТТ»ПЯ¶У¶УФұІОјУұИИь°ьә¬өД»щұҫКВјюёцКэ![]() Ј¬
Ј¬
ЎаЗЎәГУР3Гы№ъјТТ»ПЯ¶У¶УФұІОјУұИИьөДёЕВКp![]() .
.
(2)![]() өДИЎЦөОӘ0Ј¬1Ј¬2Ј¬3Ј¬4Ј¬
өДИЎЦөОӘ0Ј¬1Ј¬2Ј¬3Ј¬4Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ЎаXөД·ЦІјБРОӘЈә
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
(3)![]() »сКӨөДёЕВК
»сКӨөДёЕВК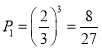 Ј¬
Ј¬
![]() »сКӨөДёЕВК
»сКӨөДёЕВК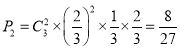 Ј¬
Ј¬
![]() »сКӨөДёЕВК
»сКӨөДёЕВК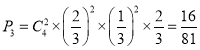 Ј¬
Ј¬
ЛщТФБЦёЯФ¶»сөГ№ЪҫьөДёЕВКОӘ![]() .
.



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝНЦФІ![]() өДАлРДВКОӘ
өДАлРДВКОӘ![]() Ј¬ТФФӯөгОӘФІРДЈ¬НЦФІ¶М°лЦбіӨОӘ°лҫ¶өДФІУлЦұПЯ
Ј¬ТФФӯөгОӘФІРДЈ¬НЦФІ¶М°лЦбіӨОӘ°лҫ¶өДФІУлЦұПЯ![]() ПаЗРЈ®
ПаЗРЈ®
ЈЁ1Ј©ЗуНЦФІөД·ҪіМЈ»
ЈЁ2Ј©MЈ¬NКЗНЦФІЙП№ШУЪxЦб¶ФіЖөДБҪөгЈ¬PКЗНЦФІЙПІ»Н¬УЪMЈ¬NөДТ»өгЈ¬ЦұПЯPMЈ¬PNҪ»xЦбУЪDЈЁxDЈ¬0Ј©EЈЁxEЈ¬0Ј©Ј¬ЦӨГчЈәxDxEОӘ¶ЁЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЦұҪЗЧшұкПөxOyЦРЈ¬ТФЧшұкФӯөгOОӘј«өгЈ¬ТФxЦбХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯCөДј«Чшұк·ҪіМОӘҰС2©Ғ4ҰСsinЈЁҰИ![]() Ј©ЈҪ0Ј®
Ј©ЈҪ0Ј®
ЈЁ1Ј©ЗуЗъПЯCөДЦұҪЗЧшұк·ҪіМЈ»
ЈЁ2Ј©ИфЦұПЯlөДІОКэ·ҪіМКЗ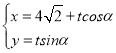 ЈЁҰБОӘІОКэЈ©Ј¬ЗТҰБЎКЈЁ
ЈЁҰБОӘІОКэЈ©Ј¬ЗТҰБЎКЈЁ![]() Ј¬ҰРЈ©КұЈ¬ЦұПЯlУлЗъПЯCУРЗТЦ»УРТ»ёцҪ»өгPЈ¬ЗуөгPөДј«ҫ¶Ј®
Ј¬ҰРЈ©КұЈ¬ЦұПЯlУлЗъПЯCУРЗТЦ»УРТ»ёцҪ»өгPЈ¬ЗуөгPөДј«ҫ¶Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЛ«ЗъПЯ![]() Јә
Јә![]() ЈЁ
ЈЁ![]() Ј¬
Ј¬![]() Ј©өДЧуЎўУТҪ№өг·ЦұрОӘ
Ј©өДЧуЎўУТҪ№өг·ЦұрОӘ![]() Ј¬
Ј¬![]() Ј¬№эөг
Ј¬№эөг![]() ЗТРұВКОӘ
ЗТРұВКОӘ![]() өДЦұПЯҪ»Л«ЗъПЯУЪ
өДЦұПЯҪ»Л«ЗъПЯУЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬ПЯ¶О
БҪөгЈ¬ПЯ¶О![]() өДҙ№ЦұЖҪ·ЦПЯЗЎ№эөг
өДҙ№ЦұЖҪ·ЦПЯЗЎ№эөг![]() Ј¬ФтёГЛ«ЗъПЯөДАлРДВКОӘЈЁ Ј©
Ј¬ФтёГЛ«ЗъПЯөДАлРДВКОӘЈЁ Ј©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЦРРДФЪФӯөг![]() Ј¬Ҫ№өгФЪ
Ј¬Ҫ№өгФЪ![]() ЦбЙПЈ¬АлРДВКОӘ
ЦбЙПЈ¬АлРДВКОӘ![]() өДНЦФІ№эөг
өДНЦФІ№эөг![]()

ЈЁ1Ј©ЗуНЦФІөД·ҪіМЈ»
ЈЁ2Ј©ЙиІ»№эФӯөг![]() өДЦұПЯ
өДЦұПЯ![]() УлёГНЦФІҪ»УЪ
УлёГНЦФІҪ»УЪ![]() БҪөгЈ¬ВъЧгЦұПЯ
БҪөгЈ¬ВъЧгЦұПЯ![]() өДРұВКТАҙОіЙөИұИКэБРЈ¬Зу
өДРұВКТАҙОіЙөИұИКэБРЈ¬Зу![]() Гж»эөДИЎЦө·¶О§Ј®
Гж»эөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪАвіӨОӘ1өДХэ·ҪМе![]() ЦРЈ¬EЈ¬F·ЦұрОӘПЯ¶ОCDәН
ЦРЈ¬EЈ¬F·ЦұрОӘПЯ¶ОCDәН![]() ЙПөД¶ҜөгЈ¬ЗТВъЧг
ЙПөД¶ҜөгЈ¬ЗТВъЧг![]() Ј¬ФтЛДұЯРО
Ј¬ФтЛДұЯРО![]() ЛщО§іЙөДНјРОЈЁИзНјЛщКҫТхУ°Іҝ·ЦЈ©·ЦұрФЪёГХэ·ҪМеУР№«№І¶ҘөгөДИэёцГжЙПөДХэН¶У°өДГж»эЦ®әНЈЁЎЎЎЎЈ©
ЛщО§іЙөДНјРОЈЁИзНјЛщКҫТхУ°Іҝ·ЦЈ©·ЦұрФЪёГХэ·ҪМеУР№«№І¶ҘөгөДИэёцГжЙПөДХэН¶У°өДГж»эЦ®әНЈЁЎЎЎЎЈ©

A. УРЧоРЎЦө![]() B. УРЧоҙуЦө
B. УРЧоҙуЦө![]() C. ОӘ¶ЁЦө3D. ОӘ¶ЁЦө2
C. ОӘ¶ЁЦө3D. ОӘ¶ЁЦө2
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]()
![]() өДТ»ёцҪ№өгОӘ
өДТ»ёцҪ№өгОӘ![]() Ј¬ЧуУТ¶Ҙөг·ЦұрОӘ
Ј¬ЧуУТ¶Ҙөг·ЦұрОӘ![]() .ҫӯ№эөг
.ҫӯ№эөг![]() өДЦұПЯ
өДЦұПЯ![]() УлНЦФІ
УлНЦФІ![]() Ҫ»УЪ
Ҫ»УЪ![]() БҪөг.
БҪөг.
ЈЁ1Ј©ЗуНЦФІ·ҪіМј°АлРДВК.
ЈЁ2Ј©өұЦұПЯ![]() өДЗгРұҪЗОӘ
өДЗгРұҪЗОӘ![]() КұЈ¬ЗуПЯ¶О
КұЈ¬ЗуПЯ¶О![]() өДіӨЈ»
өДіӨЈ»
ЈЁ3Ј©јЗ![]() өДГж»э·ЦұрОӘ
өДГж»э·ЦұрОӘ![]() әН
әН![]() Ј¬Зу
Ј¬Зу![]() ЧоҙуЦө.
ЧоҙуЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪХэ·ҪМеABCD©ҒA1B1C1D1ЦРЈ¬EЈ¬F·ЦұрКЗАвAA1Ј¬ADЙПөДөгЈ¬ЗТAE=EA1Ј¬AF![]() FD.
FD.
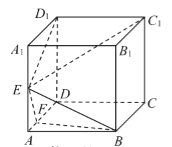
ЈЁ1Ј©ЗуЦӨЈәЖҪГжEC1D1ЎНЖҪГжEFBЈ»
ЈЁ2Ј©Зу¶юГжҪЗE©ҒFB©ҒAөДУаПТЦө.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com