A
分析:根据题意画出图形,过圆心A作AB垂直于已知直线,垂足为B,与圆交于点C,根据图形可知当动点P运动到C位置时,到已知直线的距离最短,最短距离为|CB|,所以利用点到直线的距离公式求出圆心A到已知直线的距离,即为|AB|的长,由|AB|减去圆的半径|AC|的长即可求出|CB|的长,即为最短距离.
解答:根据题意画出图形,如图所示:
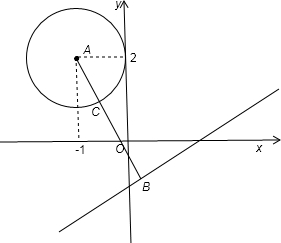
由圆的方程,得到圆心A的坐标为(-1,2),半径r=1,
圆心到直线3x-4y-9=0的距离|AB|=
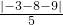
=4,
则当动点P运动到点C位置时,到已知直线的距离最短,
所以最短距离为|CB|=|AB|-|AC|=4-1=3.
故选A.
点评:此题考查了直线与圆的位置关系,点到直线的距离公式,以及数形结合的数学思想.在圆周上找出到已知直线最短的点的位置为点C是解本题的关键.


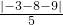 =4,
=4,
