
思路分析:将问题转化为几何概型求解.能构成一个三角形需要用三个变量来描述,我们可用这三个变量组成的有序数组来表示基本事件,利用空间直角坐标系即可建立与体积相关的几何概型.
解:令A=“三线段能构成一个三角形”.
设三线段各长为x、y、z,则每一个试验结果可表示为(x,y,z),0≤x,y,z≤a,所有可能的结果为Ω={(x,y,z)|0≤x,y,z≤a}.
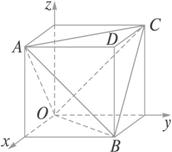
图3-3-8
因为三线段构成一个三角形的条件是:x+y>z,x+z>y,y+z>x,
所以A={(x,y,z)|x+y>z,x+z>y,y+z>x,0≤x,y,z≤a}是一个以O、A、B、C、D为顶点的六面体(如图338),其体积等于a3-3·![]() ·
·![]() a=
a=![]() a3.
a3.
从而P(A)=![]() =0.5.
=0.5.


科目:高中数学 来源: 题型:
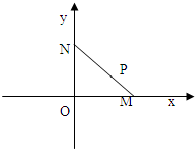 如图,线段MN的两个端点M、N分别在x轴、y 轴上滑动,|MN|=5,点P是线段MN上一点,且
如图,线段MN的两个端点M、N分别在x轴、y 轴上滑动,|MN|=5,点P是线段MN上一点,且| MP |
| 2 |
| 3 |
| PN |
| OS |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省长泰一中高二下学期期中考试理科数学 题型:解答题
(本小题满分14分)
如图,线段MN的两个端点M.N分别在x轴.y 轴上滑动, ,点P是线段MN上一点,且
,点P是线段MN上一点,且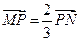 ,点P随线段MN的运动而变化.
,点P随线段MN的运动而变化.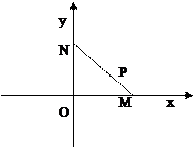
(1)求点P的轨迹C的方程;
(2)过点(2,0)作直线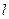 ,与曲线C交于A.B两点,O是坐标原点,设
,与曲线C交于A.B两点,O是坐标原点,设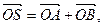 是否存在这样的直线
是否存在这样的直线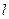 ,使四边形
,使四边形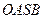 的对角线相等(即
的对角线相等(即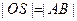 )?若存在,求出直线
)?若存在,求出直线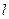 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二下学期期中考试理科数学 题型:解答题
(本小题满分14分)
如图,线段MN的两个端点M.N分别在x轴.y 轴上滑动,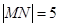 ,点P是线段MN上一点,且
,点P是线段MN上一点,且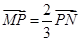 ,点P随线段MN的运动而变化.
,点P随线段MN的运动而变化.
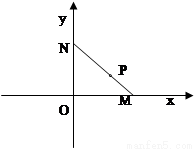
(1)求点P的轨迹C的方程;
(2)过点(2,0)作直线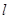 ,与曲线C交于A.B两点,O是坐标原点,设
,与曲线C交于A.B两点,O是坐标原点,设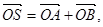 是否存在这样的直线
是否存在这样的直线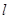 ,使四边形
,使四边形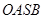 的对角线相等(即
的对角线相等(即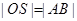 )?若存在,求出直线
)?若存在,求出直线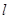 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年浙江省温州市三溪中学高二期中数学试卷(理科)(选修2-1)(解析版) 题型:解答题
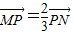 ,点P随线段MN的运动而变化.
,点P随线段MN的运动而变化.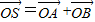 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.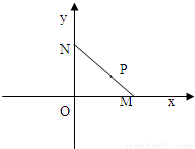
查看答案和解析>>
科目:高中数学 来源:2007-2008学年浙江省宁波二中、温州市永嘉十五中等三校联考高二(下)期中数学试卷(选修2-1)(解析版) 题型:解答题
 ,点P随线段MN的运动而变化.
,点P随线段MN的运动而变化. ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com