
分析 首先分析题目已知不等式|3x-b|<4的解集中的整数有且仅有1,2,3,求t的取值范围,考虑到先根据绝对值不等式的解法解出|3x-b|<4含有参数t的解,使得解中只有整数1,2,3,即限定左边大于或等于0小于1,右边大于3小于或等于4.即可得到答案.
解答 解:∵|3x+t|<4,等价于-4<3x+t<4,
等价于-4-t<3x<4-t,即 $\frac{-4-t}{3}$<x<$\frac{4-t}{3}$.
∵解集中的整数有且仅有1,2,3,则$\left\{\begin{array}{l}{0≤\frac{-4-t}{3}<1}\\{3<\frac{4-t}{3}≤4}\end{array}\right.$,求得-7<t<-5,
故答案为:(-7,-5).
点评 此题主要考查绝对值不等式的解法问题,题目涵盖知识点少,计算量小,属于中档题.


科目:高中数学 来源: 题型:解答题
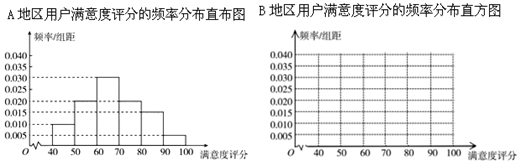
| 满意度 评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 2 | 8 | 14 | 10 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{1}{4})∪[{2,+∞})$ | B. | $[{-\frac{1}{4},2})$ | C. | $[{-2,-\frac{1}{4}})$ | D. | $({-2,-\frac{1}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{25}{12}$ | C. | $\frac{9}{4}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在正方体ABCD-A1B1C1D1中E,G,H分别为BC,C1D1,AA1的中点.
在正方体ABCD-A1B1C1D1中E,G,H分别为BC,C1D1,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com