
 在正方体ABCD-A1B1C1D1中E,G,H分别为BC,C1D1,AA1的中点.
在正方体ABCD-A1B1C1D1中E,G,H分别为BC,C1D1,AA1的中点.分析 (1)线面平行转化为证明线线平面,连结AC交BD于O连结DO,OE,E,G,H分别为BC,C1D1,AA1的中点,可证四边形OEGD1为平行四边形,可得EG∥平面BDD1B1
(2)找到异面直线的平面角,延长DB于M,连结B1M,HM,∠HB1M为所求角,利用余弦定理可得角的大小.
解答 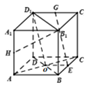 解:(1)证明:ABCD-A1B1C1D1是正方体,E,G,H分别为BC,C1D1,AA1的中点,
解:(1)证明:ABCD-A1B1C1D1是正方体,E,G,H分别为BC,C1D1,AA1的中点,
连结AC交BD于O连结DO,OE,
∵$OE\underline{\underline∥}\frac{1}{2}CD,OD\underline{\underline∥}{D_1}G$
∴四边形OEGD1为平行四边形
∴EG∥OD1,又EG?面BDD1B1,OD1?面BDD1B1,
∴EG∥平面BDD1B1.
(2)延长DB于M,使$BM=\frac{1}{2}BD$,
连结B1M,HM,∠HB1M为所求角.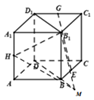
设正方体边长为1,则${B_1}M=\frac{{\sqrt{6}}}{2},{B_1}H=\frac{{\sqrt{5}}}{2},AM=\frac{{\sqrt{10}}}{2},HM=\frac{{\sqrt{11}}}{2}$,
∴cos∠HB1M=0,
∴B1H与EG所成的角为90°.
点评 本题考查了线面平行的证明,只需要证明这条直线平行于平面内的一条直线即可.异面直线的角,要找到它们在同一个平面的角,通过平移,中位线,延长相交等求解.属于基础题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分接近$\sqrt{5}$的所有实数 | B. | 所有的正方形 | ||
| C. | 著名的数学家 | D. | 1,2,3,3,4,4,4,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$.A为椭圆上异于顶点的一点,点P满足$\overrightarrow{OP}$=$2\overrightarrow{AO}$,
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$.A为椭圆上异于顶点的一点,点P满足$\overrightarrow{OP}$=$2\overrightarrow{AO}$,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com