
����Ŀ���ס�����λ����Ա����̨�����ϸ�������A��B�������͵��ļ��IJ������ֲ���ʹ�������ļ���Ϊ��Ʒ����֪A�ļ���Ҫ������0.5Сʱ��������0.2Сʱ��B�ļ���Ҫ������0.3Сʱ��������0.6Сʱ����һ���������У�������ֻ������6Сʱ��������ֻ������8Сʱ��A�ļ�ÿ�ݵ�����Ϊ60Ԫ��B�ļ�ÿ�ݵ�����Ϊ80Ԫ����ס�����λ����Ա��һ���������ڻ�õ����������Ԫ��
���𰸡�1200
���������⣺������A��Ʒx����B��Ʒy������������ΪԪz��
��x��y����Լ������ 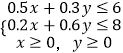 ��
��
��������Ϊz=60x+80y��x��N��y��N����
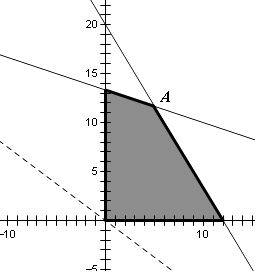
������������ͼ��ʾ��
��z=0����ֱ��l0��3x+4y=0��ƽ�ƴ�ֱ�ߣ��ڵ�A��
zȡ�����ֵ ����8�֣�
�ɷ����� ![]() ��
��
���A��4��12��
��zmax=60��4+80��12=1 200��
�������ײ�Ʒ3�����Ҳ�Ʒ2��ʱ���������Ϊ1200Ԫ��
���Դ��ǣ�1200��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������f��x��= ![]() x2+ax��g��x��=2a2lnx+b�й����㣬���ڸõ㴦����ͬ�����ߣ���a�ʣ�0��+�ޣ�ʱ��ʵ��b�����ֵ�ǣ� ��
x2+ax��g��x��=2a2lnx+b�й����㣬���ڸõ㴦����ͬ�����ߣ���a�ʣ�0��+�ޣ�ʱ��ʵ��b�����ֵ�ǣ� ��
A.e ![]()
B.2e ![]()
C.e ![]()
D.![]() e
e ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() +
+ ![]() =1 ��a��b��0 �� ������ P��1��
=1 ��a��b��0 �� ������ P��1�� ![]() ���������� e=
���������� e= ![]()
��������ԲC�ı����̣�
���������E��0����2 �� ��ֱ��l ��C�ཻ��P��Q���㣬���OPQ ��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������S��ABCD�ĵ���ABCD�������Σ������ⳤ�����ı߳�����ȣ�MΪSA���е㣬��ֱ��BM��SC���ɵĽǵ�����ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|x��a|+3x������a��0�� ����a=1ʱ����ʽf��x����3x+2�Ľ⼯
����������ʽf��x����0�Ľ⼯Ϊ{x|x�ܩ�1}����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2+ax��lnx��a��R��
��1����a=0ʱ������y=f��x���ڵ㣨1��f��1�����������߷��̣�
��2��������f��x����[1��2]���Ǽ���������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com