
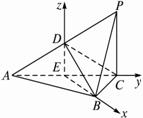
(1)D在运动过程中,是否有可能使得AP⊥面BCD?请说明理由;
(2)若D是AP的中点,求:
①异面直线CD与PB所成的角;
②直线BD与面PBC所成的角.
解:取AC的中点E,连结DE、BE则DE∥PC,BE⊥AC,?
∴DE⊥面ABC.?
如图建立的空间坐标系E—xyz,?

DE=![]() PC=
PC=![]() ,BE=
,BE=![]() .?
.?
∴A(0,-1,0),B(![]() ,0,0),C(0,1,0),P(0,1,2
,0,0),C(0,1,0),P(0,1,2![]() ),D(0,0,
),D(0,0, ![]() )?
)?
(1)![]() =(0,2,
=(0,2,![]() ),
),![]() =(-
=(-![]() ,1,0),?
,1,0),?
∴![]()
![]()
![]() =2≠0,∴AP不垂直于BC,∴AP不可能垂直面DBC,即不存在D点,使得AP⊥面DBC.?
=2≠0,∴AP不垂直于BC,∴AP不可能垂直面DBC,即不存在D点,使得AP⊥面DBC.?
(2)①![]() =(-
=(-![]() ,1,2
,1,2![]() ),
),![]() =(0,-1,
=(0,-1,![]() ),?
),?
∴cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() ,?
,?
∴PB与CD所成的角为60°.?
②设n=(x0,y0,z0)是平面PBC的法向量,![]() =(0,0,2
=(0,0,2![]() ),?
),?
则n·![]() =0,且n
=0,且n![]()
![]() =0,∴
=0,∴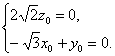
令y0=-![]() ,则
,则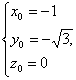 ∴n=(-1,-
∴n=(-1,-![]() ,0).?
,0).?
又![]() =(-
=(-![]() ,0,
,0, ![]() ),?
),?
∴cos〈n,![]() 〉=
〉=![]() =
=![]() =
=![]() .?
.?
∴直线BD与面PBC所成的角为arcsin![]() .
.


科目:高中数学 来源: 题型:
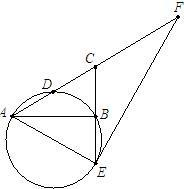 已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.
已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.查看答案和解析>>
科目:高中数学 来源: 题型:
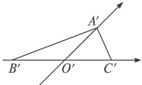 已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=
已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=
| ||
| 2 |
A、
| ||
B、2
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知(如图)在正三棱柱(底面正三角形,侧棱垂直于底面)ABC-A1B1C1中,若AB=AA1=4,点D是AA1的中点,点P是BC1中点
已知(如图)在正三棱柱(底面正三角形,侧棱垂直于底面)ABC-A1B1C1中,若AB=AA1=4,点D是AA1的中点,点P是BC1中点查看答案和解析>>
科目:高中数学 来源: 题型:
 A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.
A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.| 1 |
| 1 |
| 1 |
| 1×2 |
| 1 |
| 1×2×3 |
| 1 |
| 1×2×3×L×n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com