
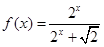 .
.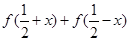 的值;
的值;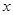 的不等式:
的不等式: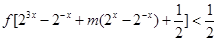 在区间
在区间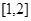 上有解,求实数
上有解,求实数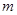 的取值范围.
的取值范围. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件: ,总有
,总有 ;(2)
;(2) ;(3) 若
;(3) 若 ,
, ,且
,且 ,则有
,则有 成立,则称
成立,则称 为“友谊函数”,请解答下列各题:
为“友谊函数”,请解答下列各题: 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;  在区间
在区间 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由. 为“友谊函数”,假定存在
为“友谊函数”,假定存在 ,使得
,使得 且
且 , 求证:
, 求证: .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.指数函数:y=2t | B.对数函数: |
| C.幂函数:y=t3 | D.二次函数:y=2t2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
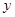 (万元)可以看成月产量
(万元)可以看成月产量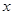 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.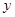 (万元)关于月产量
(万元)关于月产量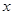 (吨)的函数关系;
(吨)的函数关系;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,若f(-4)=f(0),f(-2)=0,则关于x的不等式f(x)≤1的解集为( )
,若f(-4)=f(0),f(-2)=0,则关于x的不等式f(x)≤1的解集为( )| A.(-∞,-3]∪[-1,+∞) |
| B.[-3,-1] |
| C.[-3,-1]∪(0,+∞) |
| D.[-3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com