Question

已知等边三角形的一个顶点位于抛物线y²=x的焦点，另外两个顶点在抛物线上，则这个等边三角形的边长为    ．

Answer 1

【答案】分析：根据题意和抛物线以及正三角形的对称性，可推断出两个边的斜率，进而表示出这两条直线，与抛物线联立，求交点的坐标，从而得解．
解答：解：y²=x的焦点F（，0）
等边三角形的一个顶点位于抛物线y²=x的焦点，另外两个顶点在抛物线上，
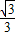
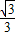
则等边三角形关于x轴对称，两个边的斜率k=±tan30°=±，其方程为：y=±（x-），
与抛物线y²=x联立，可得
∴
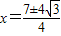
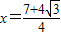
当时，，∴等边三角形的边长为
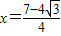
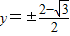
当时，，∴等边三角形的边长为
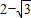
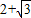
故答案为：或
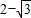点评：本题以抛物线为载体，考查抛物线与正三角形的对称性，考查学生的计算能力，属于基础题．