
| A. | 存在正数x0,当x>x0时,2x>x3 | B. | 存在正数x0,当x>x0时,x>lnx | ||
| C. | ?x>2,2x>x2 | D. | ?x>2,x3>$\sqrt{x}$ |
分析 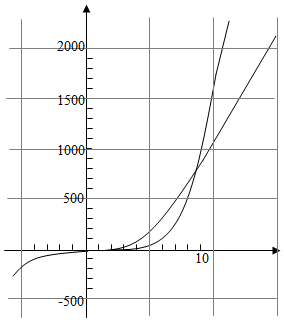 A.作出两个函数的图象,进行判断即可.
A.作出两个函数的图象,进行判断即可.
B.构造函数,求出函数的导数判断函数的单调性和极值,
C.当x=4时,不等式不成立,
D.求出不等式的等价条件进行判断.
解答 解:A.作出两个函数y=2x,y=x3的图象,由图象知存在正数x0=20,当x>20时,2x>x3成立,故A正确,
B.设f(x)=x-lnx,则f′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$,
由f′(x)>0得x>1,由f′(x)<0,得0<x<1,即当x=1时,函数取得极小值f(1)=1-ln1=1>0,
即当x>0时,f(x)>0恒成立,即x>lnx恒成立,则存在正数x0,当x>x0时,x>lnx为真命题,
C.当x=4时,2x=x2成立,则2x>x2不成立,故C错误,
D.当x>0时,由x3>$\sqrt{x}$得x6>x,即x5>1,即x>1,即当x>2时x3>$\sqrt{x}$恒成立,故D正确,
故选:C
点评 本题主要考查命题的真假判断,涉及全称命题,特称命题的真假判断,考查学生的推理和判断能力.


科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | lga>lgb | C. | 2a>2b | D. | $\frac{1}{b}$>$\frac{1}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ+μ=2 | B. | λ-μ=1 | C. | λμ=-1 | D. | λμ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com