Question

【题目】的三个内角，，所对的边分别为，，，．

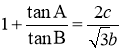（1）求的大小；

（2）若为锐角三角形，求函数的取值范围；

（3）现在给出下列三个条件：①；②；③，试从中再选择两个条件以确定，求出所确定的的面积．

Answer 1

【答案】（1）；（2）；（3）选择①②，或选择①③，.

【解析】

试题（1）因为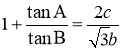，切化弦，边化角， 根据，化简整理得，； （2）因为，所以，把用表示，得关于的三角函数，再根据的范围，求出函数的取值范围即得函数的取值范围；（3）方案一：选择①②，可确定，因为，，，由余弦定理，得，利用得的面积．

方案二：选择①③，可确定，因为，或，，又，由正弦定理得边，利用得的面积．

试题解析：（1）因为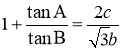，由正弦定理，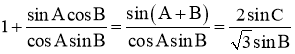

因为，，所以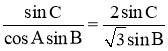

所以，

（2）因为，，所以

，

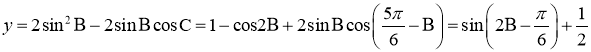又为锐角三角形，

所以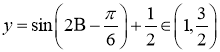

（3）方案一：选择①②，可确定，因为，，

由余弦定理，得：

整理得：，，

所以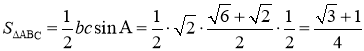

方案二：选择①③，可确定， ，

又

由正弦定理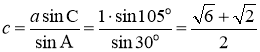

所以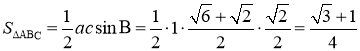

（选择②③不能确定三角形）