
【题目】设函数![]() .
.
(1)若![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(2)讨论函数![]() 的单调区间;
的单调区间;
(3)若函数![]() 的图象与
的图象与![]() 轴交于A,B两点,线段AB中点的横坐标为
轴交于A,B两点,线段AB中点的横坐标为![]() ,证明
,证明![]() .
.
【答案】(1)![]() (2)详见解析(3)证明详见解析.
(2)详见解析(3)证明详见解析.
【解析】
(1)首先求![]() ,根据解出
,根据解出![]() 的值;
的值;
(2)由(1)得![]() ,分
,分![]() 和
和![]() 两种情况讨论函数的单调区间;
两种情况讨论函数的单调区间;
(3)设出函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点的横坐标,利用分析法和根据(2)的结论进行证明,根据要证明的结论和分析的过程,利用放缩法,换元法,构造函数法解答,再利用导数求出函数的最值,即可证明.
两点的横坐标,利用分析法和根据(2)的结论进行证明,根据要证明的结论和分析的过程,利用放缩法,换元法,构造函数法解答,再利用导数求出函数的最值,即可证明.
(1)![]()
又因为![]() 的图象在
的图象在![]() 处的切线与直线
处的切线与直线![]() 平行,
平行,
即![]() ,即
,即![]() ,
,
解得:![]() ;
;
(2)由(1)得![]() ,
,
![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
①当![]() 时,对任意
时,对任意![]() ,
,![]() ,
,
![]() 此时函数
此时函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
此时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(3)不妨设![]() ,
,![]() ,且
,且![]() ,由(2)知
,由(2)知![]() ,
,
于是要证明![]() 成立,只需证:
成立,只需证:![]() ,即
,即![]() ,
,
![]() ①
①
![]() ②,
②,
①-②得![]() ,
,
![]() ,
,
故只需证明![]() ,
,
即证明![]() ,
,
即证明![]() ,变形为
,变形为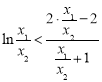 ,
,
设![]() ,令
,令![]() ,
,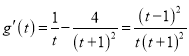 ,
,
显然当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时
时![]() ,
,
![]() 在
在![]() 上是增函数,
上是增函数,
又![]() ,
,
![]() 当
当![]() 时,
时,![]() 总成立,命题得证.
总成立,命题得证.


科目:高中数学 来源: 题型:
【题目】设f(x)=loga(1+x)+loga(3﹣x)(a>0,a≠1)且f(1)=2.
(1)求a的值及f(x)的定义域;
(2)求f(x)在区间[0,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽样100名志原者的年龄情况如下表所示.
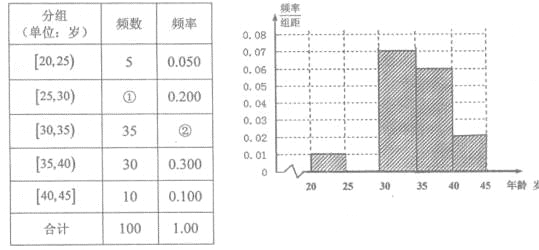
(Ⅰ)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 的三个内角
的三个内角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,
,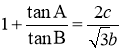 .
.
(1)求![]() 的大小;
的大小;
(2)若![]() 为锐角三角形,求函数
为锐角三角形,求函数![]() 的取值范围;
的取值范围;
(3)现在给出下列三个条件:①![]() ;②
;②![]() ;③
;③![]() ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定![]() ,求出所确定的
,求出所确定的![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系xOy中,设倾斜角为α的直线l:![]() (t为参数)与曲线C:
(t为参数)与曲线C:![]() (θ为参数)相交于不同的两点A,B.
(θ为参数)相交于不同的两点A,B.
(Ⅰ)若α=![]() ,求线段AB中点M的坐标;
,求线段AB中点M的坐标;
(Ⅱ)若|PA|·|PB|=|OP|![]() ,其中P(2,
,其中P(2,![]() ),求直线l的斜率.
),求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),经过变换
为参数),经过变换 后曲线
后曲线![]() 变换为曲线
变换为曲线![]() .
.
(1)在以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴(单位长度与直角坐标系相同)的极坐标系中,求
轴的非负半轴为极轴(单位长度与直角坐标系相同)的极坐标系中,求![]() 的极坐标方程;
的极坐标方程;
(2)求证:直线![]() 与曲线
与曲线![]() 的交点也在曲线
的交点也在曲线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,且a3+2S6=77,a10﹣a5=10.
(1)求数列{an}的通项公式;
(2)数列{bn}满足:b1=1,bn﹣bn﹣1=an﹣n+1(n≥2),求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是各项均为正数的等比数列,且b1=a1=1,b3=a4,b1+b2+b3=a3+a4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=a(|sinx|+|cosx|)﹣sin2x﹣1,a∈R.
(1)写出函数 f(x)的最小正周期(不必写出过程);
(2)求函数 f(x)的最大值;
(3)当a=1时,若函数 f(x)在区间(0,kπ)(k∈N*)上恰有2015个零点,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com