
给出命题:若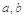 是正常数,且
是正常数,且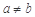 ,
,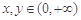 ,则
,则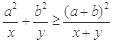 (当且仅当
(当且仅当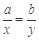 时等号成立).根据上面命题,可以得到函数
时等号成立).根据上面命题,可以得到函数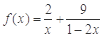 (
(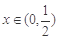 )的最小值及取最小值时的
)的最小值及取最小值时的 值分别为( )
值分别为( )
A.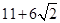 , ,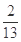 | B.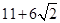 , ,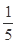 |
C.25,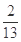 | D.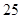 , ,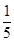 |
科目:高中数学 来源: 题型:单选题
有一段 “三段论”推理是这样的:对于可导函数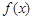 ,若
,若 ,则
,则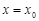 是函数
是函数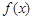 的极值点.因为
的极值点.因为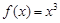 在
在 处的导数值
处的导数值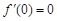 ,所以
,所以 是
是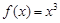 的极值点.以上推理中 ( )
的极值点.以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用数学归纳法证明1+2+3+ +n2=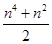 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
| A.k2+1 |
| B.(k+1)2 |
C.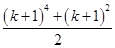 |
| D.(k2+1)+(k2+2)+ +(k+1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题:“若a,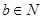 ,
,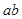 能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一个能被5整除 | D.a,b有一个不能被5整除 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com