
用反证法证明命题:“若a,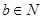 ,
,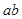 能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一个能被5整除 | D.a,b有一个不能被5整除 |
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:单选题
给出命题:若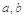 是正常数,且
是正常数,且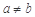 ,
,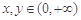 ,则
,则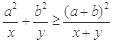 (当且仅当
(当且仅当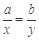 时等号成立).根据上面命题,可以得到函数
时等号成立).根据上面命题,可以得到函数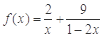 (
(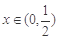 )的最小值及取最小值时的
)的最小值及取最小值时的 值分别为( )
值分别为( )
A.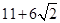 , ,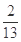 | B.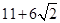 , ,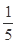 |
C.25,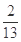 | D.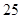 , ,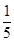 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
将正偶数 、
、 、
、 、
、 、
、 按表
按表 的方式进行排列,记
的方式进行排列,记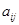 表示第
表示第 行和第
行和第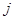 列的数,若
列的数,若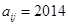 ,则
,则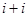 的值为( )
的值为( )
| | 第 列 列 | 第 列 列 | 第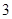 列 列 | 第 列 列 | 第 列 列 |
第 行 行 | |  |  |  |  |
第 行 行 |  | 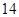 |  |  | |
第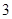 行 行 | | 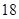 | 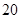 | 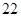 | 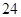 |
第 行 行 | 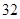 |  | 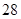 | 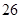 | |
第 行 行 | |  | 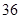 | 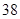 | 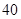 |
 |  |  |  |  |  |
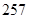 B.
B.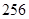 C.
C.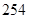 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用数学归纳法证明“n3+(n+1)3+(n+2)3(n∈N*)能被9整除”,要利用归纳假设证n=k+1时的情况,只需展开( )
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
| A.28 | B.76 | C.123 | D.199 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
有两种花色的正六边形地面砖,按下图的规律拼成若干个图案,则第六个图案中有菱形纹的正六边形的个数是( ).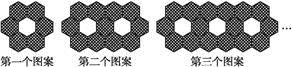
| A.26 | B.31 | C.32 | D.36 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知n是正偶数,用数学归纳法证明时,若已假设n=k(k≥2且为偶数)时命题为真,则还需证明( )
| A.n=k+1时命题成立 |
| B.n=k+2时命题成立 |
| C.n=2k+2时命题成立 |
| D.n=2(k+2)时命题成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com