
已知n是正偶数,用数学归纳法证明时,若已假设n=k(k≥2且为偶数)时命题为真,则还需证明( )
| A.n=k+1时命题成立 |
| B.n=k+2时命题成立 |
| C.n=2k+2时命题成立 |
| D.n=2(k+2)时命题成立 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:单选题
用反证法证明命题:“若a,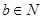 ,
,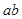 能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一个能被5整除 | D.a,b有一个不能被5整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
右图1是一个水平摆放的小正方体木块,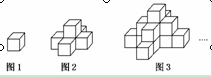
图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是( )
| A.25 | B.66 | C.91 | D.120 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
观察下列事实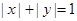 的不同整数解
的不同整数解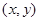 的个数为4,
的个数为4,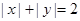 的不同整数解
的不同整数解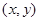 的个数为8,
的个数为8,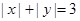 的不同整数解
的不同整数解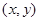 的个数为12,……,则
的个数为12,……,则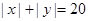 的不同整数解
的不同整数解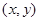 的个数为( )
的个数为( )
| A.76 | B.80 | C.86 | D.92 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用数学归纳法证明不等式“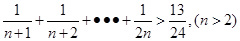 ”的过程中,由n=k到n=k+1时,不等式的左边( )
”的过程中,由n=k到n=k+1时,不等式的左边( )
A.增加了一项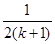 |
B.增加了两项 |
C.增加了一项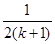 ,又减少了一项 ,又减少了一项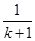 |
D.增加了两项 ,又减少了一项 ,又减少了一项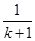 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
由集合{a1},{a1,a2},{a1,a2,a3},…的子集个数归纳出集合{a1,
a2,a3,…,an}的子集个数为( )
| A.n | B.n+1 |
| C.2n | D.2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N*,f(n)都能被m整除,则m的最大值为( )
| A.18 | B.36 | C.48 | D.54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com