
用数学归纳法证明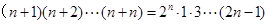 (
(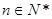 )时,从“
)时,从“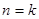 到
到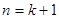 ”左边需增乘的代数式为( )
”左边需增乘的代数式为( )
A.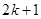 | B.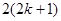 | C.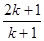 | D. |
科目:高中数学 来源: 题型:单选题
用数学归纳法证明1+2+3+ +n2=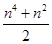 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
| A.k2+1 |
| B.(k+1)2 |
C.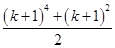 |
| D.(k2+1)+(k2+2)+ +(k+1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题:“若a,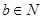 ,
,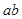 能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一个能被5整除 | D.a,b有一个不能被5整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
① ,这与三角形内角和为
,这与三角形内角和为 相矛盾,
相矛盾,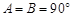 不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角
不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角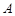 、
、 、
、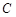 中有两个直角,不妨设
中有两个直角,不妨设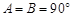 ;正确顺序的序号为 ( )
;正确顺序的序号为 ( )
| A.①②③ | B.③①② | C.①③② | D.②③① |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知集合A={3m+2n|m>n且m,n∈N},若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…,依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )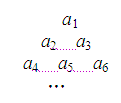
| A.247 | B.735 |
| C.733 | D.731 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
仔细观察下面○和●的排列规律:
○●○○●○○○●○○○○●○○○○○●○○○○○○ ●……
若依此规律继续下去,得到一系列的○和●,那么在前120个○和●中,●的个数是( )
| A.13 | B.14 | C.15 | D.16 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N*,f(n)都能被m整除,则m的最大值为( )
| A.18 | B.36 | C.48 | D.54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com