
已知函数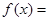
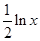
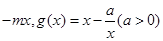 .
.
(I)求函数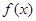 的单调区间;
的单调区间;
(Ⅱ)若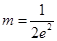 ,对
,对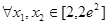 都有
都有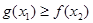 成立,求实数
成立,求实数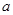 的取值范围;
的取值范围;
(Ⅲ)证明: (
(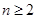 且
且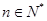 ).
).
(I)当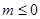 时,
时,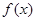 单调递增区间为(0,+∞).当m>0时,
单调递增区间为(0,+∞).当m>0时,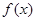 单调递增区间为(0,
单调递增区间为(0,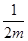 ),单调递减区间为(
),单调递减区间为(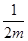 ,+∞). (Ⅱ)实数
,+∞). (Ⅱ)实数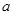 的取值范围为
的取值范围为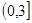 .(Ⅲ)详见解析.
.(Ⅲ)详见解析.
【解析】
试题分析:(I)应用导数研究函数的单调性.遵循“求导数,令导数大(小)于0,解不等式,求单调区间”.
(Ⅱ)将问题转化成“对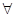
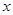
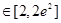 都有
都有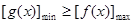 ”,
”,
通过求 ,得到函数
,得到函数 在[2,2
在[2,2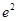 ]上是增函数,
]上是增函数,
求得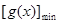 =g(2)=2-
=g(2)=2-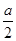 ,利用2-
,利用2-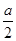
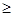
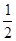 ,及
,及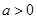 得到实数
得到实数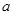 的取值范围为
的取值范围为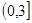 .
.
(Ⅲ)通过构造函数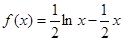 ,利用(I)确定
,利用(I)确定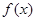 的单调性得到
的单调性得到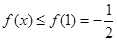 ,(当
,(当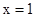 时取“=”号),利用“错位相减法”求得S=
时取“=”号),利用“错位相减法”求得S=
证得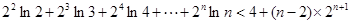 (
(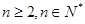 ).
).
试题解析:(I)
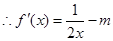 1分
1分
当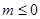 时
时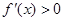 ,
,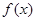 在(0,+∞)单调递增. 2分
在(0,+∞)单调递增. 2分
当m>0时,由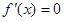 得
得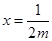
由 得
得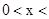
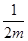
由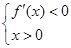 得
得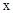 >
>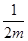 4分
4分
综上所述:当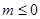 时,
时,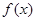 单调递增区间为(0,+∞).
单调递增区间为(0,+∞).
当m>0时,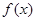 单调递增区间为(0,
单调递增区间为(0,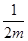 ),单调递减区间为(
),单调递减区间为(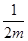 ,+∞). 5分
,+∞). 5分
(Ⅱ)若m=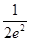 ,
,
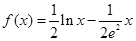 ,对
,对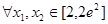 都有
都有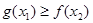 成立等价于对
成立等价于对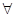
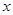
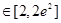 都有
都有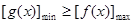 6分
6分
由(I)知在[2,2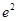 ]上
]上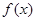 的最大值
的最大值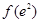 =
=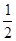 7分
7分

函数 在[2,2
在[2,2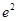 ]上是增函数,
]上是增函数,
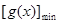 =g(2)=2-
=g(2)=2-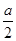 , 9分
, 9分
由2-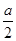
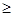
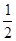 ,得
,得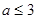 ,又因为
,又因为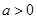 ,∴
,∴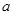 ∈
∈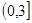
所以实数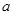 的取值范围为
的取值范围为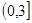 . 10分
. 10分
(Ⅲ)证明: 令m=
令m=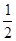 ,则
,则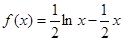
由(I)知f(x)在(0,1)单调递增,(1,+∞)单调递减,
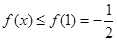 ,(当x=1时取“=”号)
,(当x=1时取“=”号)
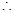
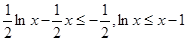 11分
11分
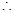
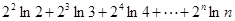
<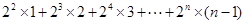 12分
12分
令S=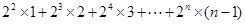 ①
①
2S=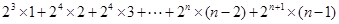 ②
②
①-②得-S=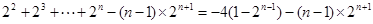
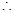 S=
S=
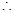
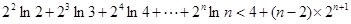 (
(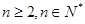 ) 14分
) 14分
考点:1、应用导数研究函数的单调性、2、最值、证明不等式,3、“错位相减法”.


科目:高中数学 来源:2012-2013学年湖北省荆州市高三(上)12月质量检查数学试卷Ⅰ(理科)(解析版) 题型:解答题
 .
. ,,求△ABC的面积.
,,求△ABC的面积.查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省临沂市临沭县高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省实验中学高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012年天津市河北区高考数学一模试卷(理科)(解析版) 题型:解答题
 .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com