
(1)������{xn}��{yn}��ͨ�
(2)��![]() xn��
xn��![]() yn��
yn��
(3)����{xn},{yn}����������ʱ������=��ʱ�����(xn,yn)�Ĵ��ڷ�Χ��
(4)����{xn},{yn}����������ʱ�����¡ݦ�2ʱ������(xn,yn)�Ĵ��ڷ�Χ��ͼ�α�ʾ����.
�⣺(1)�������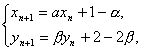 ��
��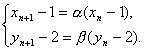
��{xn-1}��{yn-2}�ǹ��ȷֱ�Ϊ��,�µĵȱ�����.
�� ��
��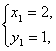
��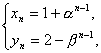 n=1ʱҲ����.
n=1ʱҲ����.
(2)��0������1,0���£�1,��![]() xn=1,
xn=1,![]() yn=2.
yn=2.
(3)(x1,y1)=(2,1),2��k��nʱ���ɦ�=��,xk=1+��k-1,yk=2-��k-1.
��ȥ��k-1��xk+yk=3,��k��2��0������1,
���(xn,yn)���߶�x+y=3(1��x��2)��.

(4)(x1,y1)=(2,1),2��k��nʱ,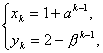 k-1��0,
k-1��0,
��(2)��1��xk��2,1��yk��2,��(��k-1)2=(xk-1)2,
��(��2)k-1=(xk-1)2.�ߦ¡ݦ�2,���k-1��(��2)k-1,��2-yk��(xk-1)2.
��yk��-(xk-1)2+2,���(xn,yn)���ڵķ�Χ��y��-(x-1)2+2��1��x��2,1��y��2����(2��1)����ͼ��Ϊͼ����Ӱ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| OP |
| OA |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ijУ���е���ѧ�����У�ȫ�����ѧ���ľ����ɼ����Ʒ�����̬�ֲ�![]() ����֪�ɼ���90�����ϣ���90�֣���ѧ����12����
����֪�ɼ���90�����ϣ���90�֣���ѧ����12����
�������ʴ˴β���ѧ������ԼΪ�����ˣ�
��������У�ƻ����������ɼ�����ǰ50����ѧ���������轱�ķ�����ԼΪ���ٷ֣�
�ɹ����ĵģ����֣�����̬�ֲ���![]()
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.2 1.3 1.4 1.9 2.0 2.1 | 0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 | 0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 | 0.888 0.9066 0.9222 0.9726 0.9783 0.9830 | 0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 | 0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 | 0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 | 0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 | 0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 | 0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 | 0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
��������С����Ҫ������̬�ֲ����Զ����¼��ĸ���ͱ���̬�ֲ��IJ��ģ��������ø���ͳ��֪ʶ���ʵ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ijУ���е���ѧ�����У�ȫ�����ѧ���ľ����ɼ����Ʒ�����̬�ֲ�![]() ����֪�ɼ���90�����ϣ���90�֣���ѧ����12����
����֪�ɼ���90�����ϣ���90�֣���ѧ����12����
�������ʴ˴β���ѧ������ԼΪ�����ˣ�
��������У�ƻ����������ɼ�����ǰ50����ѧ���������轱�ķ�����ԼΪ���ٷ֣�
�ɹ����ĵģ����֣�����̬�ֲ���![]()
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.2 1.3 1.4 1.9 2.0 2.1 | 0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 | 0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 | 0.888 0.9066 0.9222 0.9726 0.9783 0.9830 | 0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 | 0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 | 0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 | 0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 | 0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 | 0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 | 0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com