
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 3分)
3分)| 运输工具 | 途中速度 (km/h) | 途中费用 (元/km) | 装卸时间 (h) | 装卸费用 (元) |
| 汽车 | 50 | 8 | 2 | 1000 |
| 火车 | 100 | 4 | 4 | 2000 |
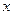 km
km 车运输的总费用分别为
车运输的总费用分别为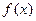 与
与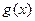 ,求
,求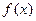 与
与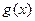 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
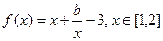
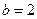 时,求
时,求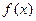 的值域;
的值域;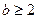 时,
时,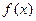 的最大值为M,最小值为m,且满足:
的最大值为M,最小值为m,且满足: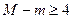 ,求b的取值范围.
,求b的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
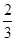 倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。
倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com