
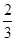 倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。
倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。科目:高中数学 来源:不详 题型:解答题
 的零点
的零点 为
为 的不动点.已知函数
的不动点.已知函数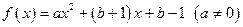
 时,求函数
时,求函数 的不动点;
的不动点; ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求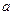
 的取值范围;
的取值范围; 有不变号零点,且
有不变号零点,且 ,求实数
,求实数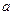 的最小值.
的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 时间 | 第4天 | 第32天 | 第60天 | 第90天 |
| 价格(千元) | 23 | 30 | 22 | 7 |
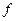 (
( )关于时间
)关于时间 的函数表达式(
的函数表达式( 表示投入市场的第
表示投入市场的第 天);
天); (
( )与时间
)与时间 的函数关系是
的函数关系是 ,求日销售额的最大值,并求第几天销售额最高?
,求日销售额的最大值,并求第几天销售额最高?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com