
 的零点
的零点 为
为 的不动点.已知函数
的不动点.已知函数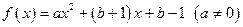
 时,求函数
时,求函数 的不动点;
的不动点; ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求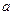
 的取值范围;
的取值范围; 有不变号零点,且
有不变号零点,且 ,求实数
,求实数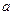 的最小值.
的最小值. 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:不详 题型:解答题
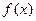 对于其定义域内的某一数
对于其定义域内的某一数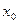 ,有
,有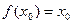 ,则称
,则称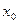 是
是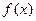 的一个不动点. 已知函数
的一个不动点. 已知函数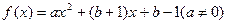 .
.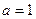 ,
,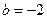 时,求函数
时,求函数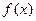 的不动点;
的不动点;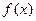 恒有两个不动点,求a的取值范围;
恒有两个不动点,求a的取值范围;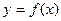
 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数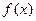 的不动点,且A、B的中点C在函数
的不动点,且A、B的中点C在函数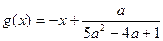 的图象上,求b的最小值.
的图象上,求b的最小值.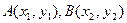 的中点坐标为
的中点坐标为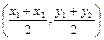 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
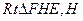 是直角
是直角 顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,
顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,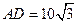 米,记
米,记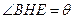 。
。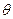 的函数,并写出定义域;
的函数,并写出定义域;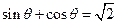 ,求此时管道的长度L;
,求此时管道的长度L;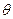 取何值时,污水净化效果最好?并求出此时管道的长度。
取何值时,污水净化效果最好?并求出此时管道的长度。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 3分)
3分)| 运输工具 | 途中速度 (km/h) | 途中费用 (元/km) | 装卸时间 (h) | 装卸费用 (元) |
| 汽车 | 50 | 8 | 2 | 1000 |
| 火车 | 100 | 4 | 4 | 2000 |
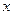 km
km 车运输的总费用分别为
车运输的总费用分别为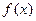 与
与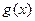 ,求
,求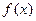 与
与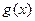 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
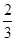 倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。
倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com