
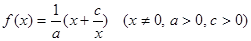 ,当
,当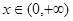 时,函数
时,函数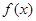 在x=2处取得最小值1。
在x=2处取得最小值1。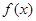
 的解析式;
的解析式;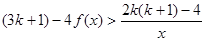 。
。 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大预计收益是多少?
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大预计收益是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的零点
的零点 为
为 的不动点.已知函数
的不动点.已知函数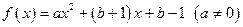
 时,求函数
时,求函数 的不动点;
的不动点; ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求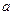
 的取值范围;
的取值范围; 有不变号零点,且
有不变号零点,且 ,求实数
,求实数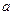 的最小值.
的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
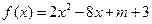 为
为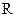 上的连续函数
上的连续函数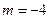 ,判断
,判断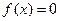 在
在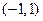 上是否有零根存在?没有,请说明理由;若有,并在精确度为
上是否有零根存在?没有,请说明理由;若有,并在精确度为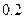 的条件下(即根所在区间长度小于
的条件下(即根所在区间长度小于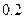 ),用二分法求出使这个零根
),用二分法求出使这个零根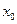 存在的小区间;
存在的小区间;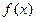 在区间
在区间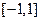 上存在零点,求实数
上存在零点,求实数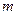 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且 在区间
在区间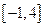 上的最大值是12.
上的最大值是12.  的解析式;
的解析式; 使得方程
使得方程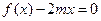 在区间
在区间 内有且只有两个不等的
内有且只有两个不等的 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com