
科目:高中数学 来源:不详 题型:单选题
| 单价(元/kg) | 2 | 2.4 | 2.8 | 3.2 | 3.6 | 4 |
| 供给量(1000kg) | 50 | 60 | 70 | 75 | 80 | 90 |
| 单价(元/kg) | 4 | 3.4 | 2.9 | 2.6 | 2.3 | 2 |
| 需求量(1000kg) | 50 | 60 | 65 | 70 | 75 | 80 |
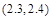 内 B.
内 B.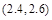 内 C.
内 C.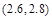 内 D.
内 D.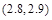 内
内查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
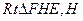 是直角
是直角 顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,
顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,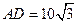 米,记
米,记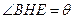 。
。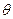 的函数,并写出定义域;
的函数,并写出定义域;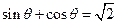 ,求此时管道的长度L;
,求此时管道的长度L;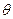 取何值时,污水净化效果最好?并求出此时管道的长度。
取何值时,污水净化效果最好?并求出此时管道的长度。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ),定义运算"⊙"为(a,b)⊙(c,d)=(a+c,bd),且(x,1)⊙(2,y)
),定义运算"⊙"为(a,b)⊙(c,d)=(a+c,bd),且(x,1)⊙(2,y) =(4,2),则(x,y)为.
=(4,2),则(x,y)为. | A.(1,1) | B.(1,2) | C.( 2,1) 2,1) | D.(2,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com