
| 单价(元/kg) | 2 | 2.4 | 2.8 | 3.2 | 3.6 | 4 |
| 供给量(1000kg) | 50 | 60 | 70 | 75 | 80 | 90 |
| 单价(元/kg) | 4 | 3.4 | 2.9 | 2.6 | 2.3 | 2 |
| 需求量(1000kg) | 50 | 60 | 65 | 70 | 75 | 80 |
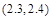 内 B.
内 B.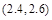 内 C.
内 C.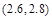 内 D.
内 D.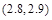 内
内

科目:高中数学 来源:不详 题型:单选题
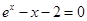 的一个根所在的区间为
的一个根所在的区间为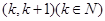 ,则k的值为( )
,则k的值为( )| A.-1 | B.0 | C.1 | D.2 |
| x | -1 | 0 | 1 | 2 | 3 |
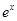 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 该产品销售量(亦即该产品的年产量)
该产品销售量(亦即该产品的年产量)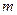 万件
万件 与年促销费用
与年促销费用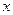 万元(
万元(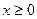 )满足
)满足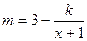 (
(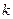 为常数).已知2011年生产该产品的前期投入需要8万元,每生产1万件该产品需要再投入16万元,企业将每件该产品的销售价格定为每件产品年平均成本的1.5倍(定价不考虑促销成本).
为常数).已知2011年生产该产品的前期投入需要8万元,每生产1万件该产品需要再投入16万元,企业将每件该产品的销售价格定为每件产品年平均成本的1.5倍(定价不考虑促销成本). 促销费用最少是多少?
促销费用最少是多少?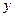 (万元)表示为年促销费用
(万元)表示为年促销费用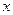 (万元)的函数,并求2011年的最大利润.
(万元)的函数,并求2011年的最大利润.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大预计收益是多少?
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大预计收益是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
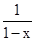 一个零点.若
一个零点.若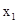 ∈(1,
∈(1,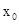 ),
), ∈(
∈(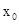 ,+
,+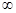 )
)A.f(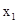 )<0,f( )<0,f( )<0 )<0 | B.f(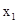 )<0,f( )<0,f( )>0 )>0 |
C.f(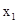 )>0,f( )>0,f( )<0 )<0 | D.f(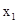 )>0,f( )>0,f( )>0 )>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com