练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．0-9共10个数字，可以组成以下多少个无重复数字的数．
    （1）五位数；
    （2）大于或等于30000的五位数；
    （3）在无重复数字的五位数中，50124从大到小排第几位？

    分析 （1）考虑首位不为0，问题得以解决；
    （2）先排首位，其它任意排，
    （3）先求出比50000大的数的个数，即可找到50124从大到小排第几．

    解答 解：（1）由题意，五位数有$9{A}_{9}^{4}$=27216．…（3分）
    （2）由题意可知最高位从3，4，5，6，7，8，9中选取，后四位任意排列，∴大于或等于30000的五位数有${C}_{7}^{1}{A}_{9}^{4}$=21168；    …（6分）
    （3）中首先确定最高位为5，6，7，8，9时的五位数个数，首位是5的五位数中50124由大到小排倒数第二个，排在第${C}_{5}^{1}{A}_{9}^{4}$-1=15119位  …（10分）

    点评 本题考查了排列组合中的数字问题，关键是掌握0不在首位，考查了分析问题，解决问题的能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    15．$\int_2^3{（{\sqrt{（{2-x}）（{x-4}）}-{2^x}}）}dx$=$\frac{π}{4}-\frac{4}{ln2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．把一根直径是20厘米，长是2米的圆柱形木材锯成同样的3段，表面积增加了400π平方厘米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设函数f（x）=ex，g（x）=ax2+bx+1．
    （1）若函数f（x）与g（x）在x=0处的切线重合，求b的值；
    （2）令h（x）=f′（x）-g′（x），求h（x）在[0，1]上的最小值；
    （3）当b=1时，若不等式f（x）＞g（x）对任意x∈（0，+∞）都成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．小明和电脑进行一次答题比赛，共4局，每局10分，现将小明和电脑的4局比赛的得分统计如表：
    小明5768
    电脑69510
    （1）求小明和电脑在本次比赛中的平均得分x1，x2及方差s12，s22；
    （2）从小明和电脑的4局比赛得分中随机各选取1个分数，并将其得分分别记为m，n，求|m-n|＞2的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点为F1，F2，离心率为$\frac{{\sqrt{3}}}{3}$，过F2的直线l交C于A，B两点，若△ABF1的周长为4$\sqrt{3}$，则C的短轴长为（　　）
    A．2B．$2\sqrt{2}$C．4D．$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=$\frac{x}{lnx}$+mx（m为常数）．
    （1）若y=f（x）在x=e2处的切线与直线4x+9y-2016=0垂直，求y=f（x）的单调区间；
    （2）若不等式f（x）≤$\frac{{e}^{2}}{2}$在[e，e2]上值成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

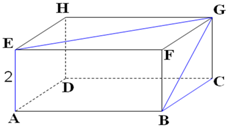    14．如图，已知长方体ABCD-EFGH中，AB=AD=2$\sqrt{3}$，AE=2
    （1）求BC和EG所成的角是多少度？
    （2）求AE和BG所成的角是多少度？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．某学校用系统抽样的方法，从全校500名学生中抽取50名做问卷调查，现将500名学生编号为1，2，3，…，500，在1～10中随机抽地抽取一个号码，若抽到的是3号，则从11～20中应抽取的号码是（　　）
    A．14B．13C．12D．11

    查看答案和解析>>

    同步练习册答案