分析:①若
2=,则|
|=|
|;②使
=成立的充分条件是
与
同向;③“|
+
|=|
|-|
|”是“?λ∈R,使得
=λ”的不充分不必要条件;④
|-|>1?
<θ<π;⑤由题设条件作出单位圆,数形结合能够作出正确判断.
解答:解:①若
2=,则|
|=|
|,故①错误;
②使
=成立的充分条件是
∥
,且
与
同向,故②错误;
③若
,
都是非零向量,
“|
+
|=|
|-|
|”⇒“
⊥”,
∴“|
+
|=|
|-|
|”是“?λ∈R,使得
=λ”的不充分不必要条件,故③错误;
④充分性:∵
,
均为单位向量,其夹角为θ,∴0≤θ≤π,
∵
|-|>1,
∴
2+2-2||||cosθ=2-2cosθ>1,
解得cos
θ<,∴
<θ<π.
必要性:∵
<θ<π,∴cosθ
<,
∴
2+2-2||||cosθ=2-2cosθ>1,
∴
|-|>1,
故“
|-|>1”是“
θ∈(,π)”的充要条件,故④正确;
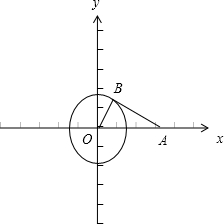
⑤∵
,
(≠,≠)满足
||=1,且
与
-的夹角为150°,
∴作出如图的单位圆,取
=,
=
,必须满足∠OAB=30°,
当AB与圆O相切时,|
|
max=|OA|=2|OB|=2,
∴
||的取值范围是(0,2],故⑤正确.
故答案为:④⑤.
点评:本题考查命题的真假判断及应用,解题时要认真审题,注意平面向量知识的合理运用.




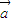 •
•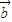 =
=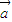 •
• 且
且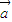 ≠
≠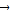 时,必有
时,必有 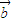 =
=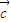 ②如
②如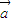 ∥
∥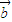 时,必存在唯一实数λ使
时,必存在唯一实数λ使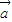 =λ
=λ ③
③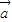 ,
,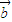 ,
,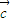 互不共线时,
互不共线时,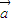 -
-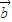 必与
必与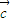 不共线④
不共线④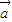 与
与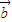 共线且
共线且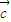 与
与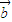 也共线时,则
也共线时,则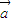 与
与 必共线其中正确命题个数有( )
必共线其中正确命题个数有( )