
【题目】如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则至少有两个数位于同行或同列的概率是( ) 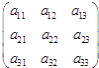
A.![]()
B.![]()
C.![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|cosx|sinx,给出下列四个说法: ① ![]() ;
;
②函数f(x)的周期为π;
③f(x)在区间 ![]() 上单调递增;
上单调递增;
④f(x)的图象关于点 ![]() 中心对称
中心对称
其中正确说法的序号是( )
A.②③
B.①③
C.①④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医生的专业能力参数K可有效衡量医生的综合能力,K越大,综合能力越强,并规定:能力参数K不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力K的频率分布直方图: 
(1)求出这个样本的合格率、优秀率;
(2)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名. ①求这2名医生的能力参数K为同一组的概率;
②设这2名医生中能力参数K为优秀的人数为X,求随机变量X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是以a为首项,q为公比的等比数列,数列{bn}满足bn=1+a1+a2+…+an(n=1,2,…),数列{cn}满足cn=2+b1+b2+…+bn(n=1,2,…).若{cn}为等比数列,则a+q=( )
A.![]()
B.3
C.![]()
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C1:ρ=2cosθ,曲线C2:ρ=(ρcosθ+4)cosθ.以极点为坐标原点,极轴为x轴正半轴建立直角坐标系xOy,曲线C的参数方程为  (t为参数). (Ⅰ)求C1 , C2的直角坐标方程;
(t为参数). (Ⅰ)求C1 , C2的直角坐标方程;
(Ⅱ)C与C1 , C2交于不同四点,这四点在C上的排列顺次为H,I,J,K,求||HI|﹣|JK||的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a2=6,a3+a6=27.
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn , 且Tn= ![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( ) 
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是4月9日
C.这12天的AQI指数值的中位数是90
D.从4日到9日,空气质量越来越好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点. 
(1)求证:BF∥平面ADP;
(2)求二面角B﹣DF﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线G:y2=2px(p>0)焦点F的直线l与抛物线G交于M、N两点(M在x轴上方),满足 ![]() ,
, ![]() ,则以M为圆心且与抛物线准线相切的圆的标准方程为( )
,则以M为圆心且与抛物线准线相切的圆的标准方程为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com