[题目]已知过抛物线G:y2=2px焦点F的直线l与抛物线G交于M.N两点.满足 . .则以M为圆心且与抛物线准线相切的圆的标准方程为( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

【题目】已知过抛物线G：y2=2px（p＞0）焦点F的直线l与抛物线G交于M、N两点（M在x轴上方），满足，，则以M为圆心且与抛物线准线相切的圆的标准方程为（）
A.
B.
C.
D.

【答案】C
【解析】解：如图，过点N作NE⊥MM′，由抛物线的定义，|MM′|=|MF|，|NN′|=|NF|．
解三角形EMN，得∠EMF= ，所以直线l的斜率为，
其方程为y= （x﹣ ），
与抛物线方程联立可得3x2﹣5px+ p2=0，
∴x1+x2= p，
∴|MN|= p= ，
∴p=2，
∴M（3，2 ），r=4，
∴圆的标准方程为（x﹣3）2+（y﹣2 ）2=16．
故选：C．

求出直线l的斜率，可得直线方程，与抛物线方程联立，利用|MN|，求出p，可得M的坐标，即可求出以M为圆心且与抛物线准线相切的圆的标准方程．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，三行三列的方阵中有9个数aij（i=1，2，3；j=1，2，3），从中任取三个数，则至少有两个数位于同行或同列的概率是（）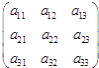
A.
B.
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】春节期间商场为活跃节日气氛，特举行“购物有奖”抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为，每次中奖可以获得20元购物代金券，方案乙的中奖率为，每次中奖可以获得30元购物代金券，未中奖则不获得购物代金券，每次抽奖中奖与否互不影响，已知小明通过购物获得了2次抽奖机会．
（1）若小明选择方案甲、乙各抽奖一次，记他累计获得的购物代金券面额之和为X，求X≤30的概率；
（2）设小明两次抽奖都选择方案甲或都选择方案乙，且都选择方案乙时，已算得，累计获得的购物代金券面额之和X1的数学期望E（X1）=24，问：小明选择这两种方案中的何种方案抽奖，累计获得的购物代金券面额之和的数学期望较大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设点P在曲线y= ex上，点Q在曲线y=ln（2x）上，则|PQ|的最小值为．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校举行“庆元旦”教工羽毛球单循环比赛（任意两个参赛队只比赛一场），共有高一、高二、高三三个队参赛，高一胜高二的概率为，高一胜高三的概率为，高二胜高三的概率为P，每场胜负独立，胜者记1分，负者记0分，规定：积分相同者高年级获胜．
（Ⅰ）若高三获得冠军概率为，求P．
（Ⅱ）记高三的得分为X，求X的分布列和期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC= AD=1，CD= ．
（1）求证：平面PQB⊥平面PAD；
（2）若二面角M﹣BQ﹣C为30°，设PM=tMC，试确定t的值．