练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．写出命题“若a2＞b2，则|a|＞|b|”的逆命题若|a|＞|b|，则a2＞b2．

    分析 根据逆命题的定义进行求解即可．

    解答 解：根据逆命题的定义得命题的逆命题为：若|a|＞|b|，则a2＞b2；
    故答案为：若|a|＞|b|，则a2＞b2

    点评 本题主要考查四种命题的关系，根据逆命题的定义是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

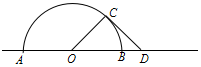    10．某公园内直线道路旁有一半径为10米的半圆形荒地（圆心O在道路上，AB为直径），现要在荒地的基础上改造出一处景观．在半圆上取一点C，道路上B点的右边取一点D，使OC垂直于CD，且OD的长不超过20米．在扇形区域AOC内种植花卉，三角形区域OCD内铺设草皮．已知种植花卉的费用每平方米为200元，铺设草皮的费用每平方米为100元．
    （1）设∠COD=x（单位：弧度），将总费用y表示为x的函数式，并指出x的取值范围；
    （2）当x为何值时，总费用最低？并求出最低费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=ax-1（a＞0且a≠1）的图象过定点A，则点A为（　　）
    A．（0，-1）B．（0，1）C．（-1，1）D．（1，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．如图正方体ABCD-A1B1C1D1，M，N分别为A1D1和AA1的中点，则下列说法中正确的个数为（　　）
    ①C1M∥AC；
    ②BD1⊥AC；
    ③BC1与AC的所成角为60°；
    ④B1A1、C1M、BN三条直线交于一点．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

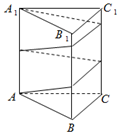    15．已知正三棱柱ABC-A1B1C1的底面边长为2cm，高为4cm，则一质点自点A出发，沿着三棱柱的侧面，绕行两周到达点A1的最短路线的长为（　　）
    A．4$\sqrt{10}$cmB．12$\sqrt{3}$cmC．2$\sqrt{13}$cmD．13cm

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．若函数$f（x）=\frac{1}{3}{x^3}-{x^2}-3x-a$有三个不同的零点，则实数a的取值范围是$（-9，\frac{5}{3}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=ex，g（x）=-x2+2x-af（x）（a∈R），x1，x2是两个任意实数且x1≠x2．
    （1）求函数f（x）的图象在x=0处的切线方程；
    （2）若函数g（x）在R上是增函数，求a的取值范围；
    （3）求证：$f（\frac{{{x_1}+{x_2}}}{2}）＜\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知函数f（x）=sin2xcos2φ+cos2xsin2φ（φ＞0）的图象关于直线x=$\frac{π}{3}$对称，则φ 的最小值为$\frac{5π}{12}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．不使用计算器，计算下列各题：
    （1）${（{5\frac{1}{16}}）^{0.5}}+{（{-1}）^{-1}}÷{0.75^{-2}}+{（{2\frac{10}{27}}）^{-\frac{2}{3}}}$；
    （2）${log_3}\sqrt{27}+lg25+lg4+{7^{{{log}_7}2}}+{（{-9.8}）^0}$．

    查看答案和解析>>

    同步练习册答案