
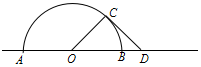
 某公园内直线道路旁有一半径为10米的半圆形荒地(圆心O在道路上,AB为直径),现要在荒地的基础上改造出一处景观.在半圆上取一点C,道路上B点的右边取一点D,使OC垂直于CD,且OD的长不超过20米.在扇形区域AOC内种植花卉,三角形区域OCD内铺设草皮.已知种植花卉的费用每平方米为200元,铺设草皮的费用每平方米为100元.
某公园内直线道路旁有一半径为10米的半圆形荒地(圆心O在道路上,AB为直径),现要在荒地的基础上改造出一处景观.在半圆上取一点C,道路上B点的右边取一点D,使OC垂直于CD,且OD的长不超过20米.在扇形区域AOC内种植花卉,三角形区域OCD内铺设草皮.已知种植花卉的费用每平方米为200元,铺设草皮的费用每平方米为100元.分析 (1)根据扇形面积公式和三角形面积公式写出函数y的解析式;
(2)利用导数判断函数的单调性,求出函数y的最小值以及对应x的值.
解答 解:(1)因为扇形AOC的半径为10 m,∠AOC=π-x(rad),
所以扇形AOC的面积为
${S_{扇AOC}}=\frac{{(π-x)•1{0^2}}}{2}=50(π-x)$,$0<x≤\frac{π}{3}$;…(3分)
在Rt△COD中,OC=10,CD=10tanx,
所以△COD的面积为
S△COD=$\frac{1}{2}$•OC•CD=50tanx;…(5分)
所以y=100S△COD+200S扇形AOC=5000(tanx+2π-2x),$0<x≤\frac{π}{3}$;…(8分)
(注:没有x的范围,扣1分)
(2)设$f(x)=tanx+2π-2x,0<x≤\frac{π}{3}$,
则$f(x)=\frac{sinx}{cosx}+2π-2x$,
$f'(x)=\frac{{{{cos}^2}x+{{sin}^2}x}}{{{{cos}^2}x}}-2=\frac{{1-2{{cos}^2}x}}{{{{cos}^2}x}}$,
令f'(x)=0,解得$x=\frac{π}{4}$,…(11分)
从而当$0<x<\frac{π}{4}$时,f'(x)<0;
当$\frac{π}{4}<x<\frac{π}{3}$,f′(x)>0;
因此f(x)在区间$(0,\frac{π}{4})$上单调递减;在区间$(\frac{π}{4},\frac{π}{3})$上单调递增;
当$x=\frac{π}{4}$时,f(x)取得最小值,
且$f(\frac{π}{4})=1+2π-\frac{π}{2}=1+\frac{3π}{2}$;…(14分)
所以y的最小值为(5000+7500π)元; …(15分)
答:当$x=\frac{π}{4}$时,改造景观的费用最低,最低费用为(5000+7500π)元. …(16分)
点评 本题考查了函数模型的应用问题,也考查了利用导数求函数的单调性与最值问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=2$\sqrt{2}$ | C. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com