
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$-$\frac{1}{2}$i | B. | $\frac{3}{2}$+$\frac{1}{2}$i | C. | 1+$\frac{1}{2}$i | D. | 1-$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
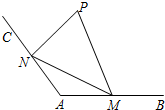 如图,洪泽湖湿地为拓展旅游业务,现准备在湿地内建造一个观景台P,已知射线AB,AC为湿地两边夹角为120°的公路(长度均超过2千米),在两条公路AB,AC上分别设立游客接送点M,N,从观景台P到M,N建造两条观光线路PM,PN,测得AM=2千米,AN=2千米.
如图,洪泽湖湿地为拓展旅游业务,现准备在湿地内建造一个观景台P,已知射线AB,AC为湿地两边夹角为120°的公路(长度均超过2千米),在两条公路AB,AC上分别设立游客接送点M,N,从观景台P到M,N建造两条观光线路PM,PN,测得AM=2千米,AN=2千米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平均说来甲队比乙队防守技术好 | |
| B. | 甲队比乙队技术水平更稳定 | |
| C. | 甲队有时表现比较差,有时表现又比较好 | |
| D. | 乙队很少不失球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com