
���� ����ץס����У���ʵ�˺�ƭ�ӵ��ص㣺��ʵ����Զ˵�滰��ƭ����Զ˵�ٻ�����������������һ�ų����ɵõ��𰸣�
��� �⣺���ĸ��˵���һ������ʵ�ˣ���Ϊ����ĸ��˶���ƭ�ӣ���˭Ҳ����˵�������ĸ���ȫ����ƭ�ӡ���
���Ե�һ��Ϊƭ�ӣ�
�ڵڶ�����Ϊƭ�ӣ���Ϊ���������ʵ�ˣ�˵ʵ�������������Ѿ��ж��˵�һ������ƭ�ӣ���ڶ��������ĸ��˶�����ʵ�ˣ�
���������˵Ļش�����ì�ܣ������˲�������ͬ��ģ��ʵڶ�����˵���Ǽٻ�������ƭ�ӣ�
���ٿ��������˵Ļش��������������ƭ�ӣ����ɢٿ�֪�����ĸ���һ������ʵ�ˣ�
��������������ʵ�ˣ���ô�����Ļ�֪���͵��ĸ�������ʵ�ˣ�
������۵���������ƭ�ӻ�����ʵ�ˣ��������Ƴ����ĸ�������ʵ�ˣ�
�ʴ�Ϊ����
���� �ų��������������г��õ�һ�ַ������������ץס�������ʵ����ƭ�ӵ��ص������һ�����ų���


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
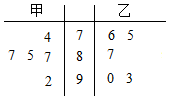 ��ij�α����У�����������ѡ�ֵĵ÷�����Ƴ���ͼ��ʾ�ľ�Ҷͼ���Ǽ����������÷�����ƽ���ֱַ�Ϊ$\overline{{x}_{��}}$��$\overline{{x}_{��}}$���������ж���ȷ���ǣ�������
��ij�α����У�����������ѡ�ֵĵ÷�����Ƴ���ͼ��ʾ�ľ�Ҷͼ���Ǽ����������÷�����ƽ���ֱַ�Ϊ$\overline{{x}_{��}}$��$\overline{{x}_{��}}$���������ж���ȷ���ǣ�������| A�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$���ױ��ҳɼ��ȶ� | B�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$���ױ��ҳɼ��ȶ� | ||
| C�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$���ұȼ׳ɼ��ȶ� | D�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$���ұȼ׳ɼ��ȶ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
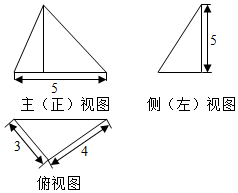
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��$\frac{5}{4}$] | B�� | ��1��$\frac{5}{4}$�� | C�� | [1��$\frac{5}{4}$] | D�� | [0��$\frac{5}{4}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2-$\sqrt{3}$ | B�� | 2$\sqrt{3}$+3 | C�� | 2+$\sqrt{3}$ | D�� | 2$\sqrt{3}$-3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com