
【题目】设数列{an}的前n项和为Sn , 且a1=a2=1,{nSn+(n+2)an}为等差数列,则a2017= .
【答案】2017?2﹣2014
【解析】解:∵a1=a2=1,{nSn+(n+2)an}为等差数列, ∴首项为:1×1+3×1=4,第二项为:2×(1+1)+4×1=8,
公差为8﹣4=4.
∴nSn+(n+2)an=4+4(n﹣1)=4n.
即nSn+(n+2)an=4n.
∴Sn=4﹣ ![]() ,
,
n≥2时,Sn﹣1=4﹣ ![]() ,
,
∴an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() ,
,
化为: ![]() =
= ![]() .
.
∴数列 ![]() 是等比数列,公比为
是等比数列,公比为 ![]() ,首项为4.
,首项为4.
∴ ![]() =4×
=4× ![]() =23﹣n .
=23﹣n .
∴an=n23﹣n .
则a2017=20172﹣2014 .
所以答案是:20172﹣2014 .
【考点精析】解答此题的关键在于理解数列的通项公式的相关知识,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点F在x轴的正半轴上,过点F的直线l与抛物线C相交于A、B两点,且满足 ![]() .
.
(1)求抛物线C的标准方程;
(2)若点M在抛物线C的准线上运动,其纵坐标的取值范围是[﹣1,1],且 ![]() ,点N是以线段AB为直径的圆与抛物线C的准线的一个公共点,求点N的纵坐标的取值范围.
,点N是以线段AB为直径的圆与抛物线C的准线的一个公共点,求点N的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c
(1)若a,b,c成等比数列, ![]() ,求
,求 ![]() 的值;
的值;
(2)若A,B,C成等差数列,且b=2,设A=α,△ABC的周长为l,求l=f(α)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有1 000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数见右上表,据此估计这1 000根中纤维长度不小于37.5 mm的根数是 .
纤维长度 | 频数 |
[22.5,25.5) | 3 |
[25.5,28.5) | 8 |
[28.5,31.5) | 9 |
[31.5,34.5) | 11 |
[34.5,37.5) | 10 |
[37.5,40.5) | 5 |
[40.5,43.5] | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.
=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.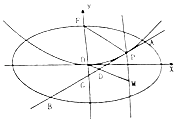
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于A,B两点且与抛物线E在第一象限相切于点P,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M,求 ![]() 的最小值及此时点P的坐标.
的最小值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1:(x﹣2)2+y2=16和圆O2:x2+y2=r2(0<r<2),动圆M与圆O1、圆O2都相切,切圆圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为e1 , e2(e1>e2),则e1+2e2的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ⊥
⊥ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |=t,若P点是△ABC所在平面内一点,且
|=t,若P点是△ABC所在平面内一点,且 ![]() =
= ![]() +
+ ![]() ,当t变化时,
,当t变化时, ![]() 的最大值等于( )
的最大值等于( )
A.﹣2
B.0
C.2
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1、F2是双曲线C: ![]() =1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )
=1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )
A.(1,+∞)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.(1, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com