
【题目】已知 ![]() ⊥
⊥ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |=t,若P点是△ABC所在平面内一点,且
|=t,若P点是△ABC所在平面内一点,且 ![]() =
= ![]() +
+ ![]() ,当t变化时,
,当t变化时, ![]() 的最大值等于( )
的最大值等于( )
A.﹣2
B.0
C.2
D.4
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的部分图象如图所示.
的部分图象如图所示.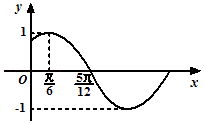
(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,若(2a﹣c)cosB=bcosC,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2 .
(1)若函数g(x)=f(x)﹣ax在其定义域内为增函数,求实数a的取值范围;
(2)在(1)的条件下,若a>1,h(x)=e3x﹣3aexx∈[0,ln2],求h(x)的极小值;
(3)设F(x)=2f(x)﹣3x2﹣kx(k∈R),若函数F(x)存在两个零点m,n(0<m<n),且2x0=m+n.问:函数F(x)在点(x0 , F(x0))处的切线能否平行于x轴?若能,求出该切线方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,左右焦点分别为F1 , F2 , 且|F1F2|=2,点(1, ![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A,B两点,且△AF2B的面积为 ![]() ,求以F2为圆心且与直线l相切的圆的方程.
,求以F2为圆心且与直线l相切的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第一组[160,164],第二组[164,168],…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图. (Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172cm以上(含172cm)的人数;
(Ⅲ)在这50名男生身高在172cm以上(含172cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为ξ,求ξ的数学期望.
参考数据:若ξ﹣N(μ,σ2),则p(μ﹣σ<ξ≤μ+σ)=0.6826,p(μ﹣2σ<ξ≤μ+2σ)=0.9544,p(μ﹣3σ<ξ≤μ+3σ)=0.9974.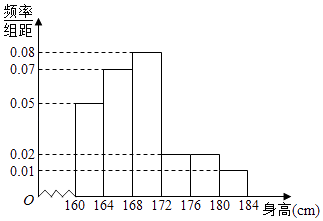
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+m|x+a|. (Ⅰ)当m=a=﹣1时,求不等式f(x)≥x的解集;
(Ⅱ)不等式f(x)≥2(0<m<1)恒成立时,实数a的取值范围是{a|a≤﹣3或a≥3},求实数m的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜率为 ![]() 的直线l与椭圆
的直线l与椭圆 ![]() +
+ ![]() =1(a>b>0)交于不同的两点A、B.若点A、B在x轴上的射影恰好为椭圆的两个焦点.
=1(a>b>0)交于不同的两点A、B.若点A、B在x轴上的射影恰好为椭圆的两个焦点.
(1)求椭圆的离心率;
(2)P是椭圆上的动点,若△PAB面积最大值是4 ![]() ,求该椭圆的方程.
,求该椭圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com