
【题目】某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第一组[160,164],第二组[164,168],…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图. (Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172cm以上(含172cm)的人数;
(Ⅲ)在这50名男生身高在172cm以上(含172cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为ξ,求ξ的数学期望.
参考数据:若ξ﹣N(μ,σ2),则p(μ﹣σ<ξ≤μ+σ)=0.6826,p(μ﹣2σ<ξ≤μ+2σ)=0.9544,p(μ﹣3σ<ξ≤μ+3σ)=0.9974.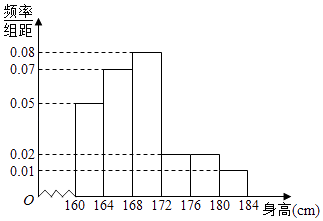
【答案】解:(Ⅰ)由直方图,经过计算该校高三年级男生平均身高为 ![]() , 高于全市的平均值168(或者:经过计算该校高三年级男生平均身高为168.72,比较接近全市的平均值168)
, 高于全市的平均值168(或者:经过计算该校高三年级男生平均身高为168.72,比较接近全市的平均值168)
(Ⅱ)由频率分布直方图知,后三组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×5=10,即这50名男生身高在172 cm以上(含172 cm)的人数为10人.
(Ⅲ)∵P(168﹣3×4<ξ≤168+3×4)=0.9974,∴ ![]() ,0.0013×100 000=130.
,0.0013×100 000=130.
所以,全市前130名的身高在180 cm以上,这50人中180 cm以上的有2人.
随机变量ξ可取0,1,2,于是 ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]()
【解析】(I)高三男生的平均身高用组中值×频率,即可得到结论;(II)首先理解频数分布直方图横纵轴表示的意义,横轴表示身高,纵轴表示频数,即:每组中包含个体的个数.我们可以依据频数分布直方图,了解数据的分布情况,知道每段所占的比例,从而求出求这50名男生身高在172cm以上(含172cm)的人数.(III)先根据正态分布的规律求出全市前130名的身高在172cm以上,这50人中172cm以上的有2人,确定ξ的可能取值,求出其概率,即可得到ξ的分布列与期望.
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+b)lnx,g(x)=alnx+ ![]() ﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
(1)求b的值;
(2)若对任意x≥1,都有g(x)> ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.
=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于A,B两点且与抛物线E在第一象限相切于点P,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M,求 ![]() 的最小值及此时点P的坐标.
的最小值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() =2csinA
=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ⊥
⊥ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |=t,若P点是△ABC所在平面内一点,且
|=t,若P点是△ABC所在平面内一点,且 ![]() =
= ![]() +
+ ![]() ,当t变化时,
,当t变化时, ![]() 的最大值等于( )
的最大值等于( )
A.﹣2
B.0
C.2
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果.《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、…、《辑古算经》等算经10部专著,有着十分丰富多彩的内容,是了解我国古代数学的重要文献.这10部专著中有7部产生于魏晋南北朝时期.某中学拟从这10部名著中选择2部作为“数学文化”校本课程学习内容,则所选2部名著中至少有一部是魏晋南北朝时期的名著的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex(a≠0),g(x)=x2(Ⅰ)若曲线c1:y=f(x)与曲线c2:y=g(x)存在公切线,求a最大值.
(Ⅱ)当a=1时,F(x)=f(x)﹣bg(x)﹣cx﹣1,且F(2)=0,若F(x)在(0,2)内有零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,其前n项和为Sn , 若S9=99,且a4 , a7 , a12成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com