
【题目】设函数f(x)=(x+b)lnx,g(x)=alnx+ ![]() ﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
(1)求b的值;
(2)若对任意x≥1,都有g(x)> ![]() ,求a的取值范围.
,求a的取值范围.
【答案】
(1)解:直线x+2y=0的斜率为﹣ ![]() ,
,
可得曲线y=f(x)在点(1,f(1))处的切线斜率为2,所以f′(1)=2,
又f′(x)=lnx+ ![]() +1,即ln1+b+1=2,所以b=1
+1,即ln1+b+1=2,所以b=1
(2)解:g(x)的定义域为(0,+∞),
g′(x)= ![]() +(1﹣a)x﹣1=
+(1﹣a)x﹣1= ![]() (x﹣1).
(x﹣1).
①若a≤ ![]() ,则
,则 ![]() ≤1,故当x∈(1,+∞)时,g′(x)>0,g(x)在(1,+∞)上单调递增.
≤1,故当x∈(1,+∞)时,g′(x)>0,g(x)在(1,+∞)上单调递增.
所以,对任意x≥1,都有g(x)> ![]() 的充要条件为g(1)>
的充要条件为g(1)> ![]() ,即
,即 ![]() ﹣1>
﹣1> ![]() ,
,
解得a<﹣ ![]() ﹣1或
﹣1或 ![]() ﹣1<a≤
﹣1<a≤ ![]()
②若 ![]() <a<1,则
<a<1,则 ![]() >1,故当x∈(1,
>1,故当x∈(1, ![]() )时,g′(x)<0;
)时,g′(x)<0;
当x∈(0,1),( ![]() ,+∞)时,g′(x)>0.
,+∞)时,g′(x)>0.
f(x)在(1, ![]() )上单调递减,在(0,1),(
)上单调递减,在(0,1),( ![]() ,+∞)上单调递增.
,+∞)上单调递增.
所以,对任意x≥1,都有g(x)> ![]() 的充要条件为g(x)>
的充要条件为g(x)> ![]() .
.
而g(x)=aln ![]() +
+ ![]() +
+ ![]() >
> ![]() 在
在 ![]() <a<1上恒成立,
<a<1上恒成立,
所以 ![]() <a<1)
<a<1)
③若a>1,g(x)在[1,+∞)上递减,不合题意.
综上,a的取值范围是(﹣∞,﹣ ![]() ﹣1)∪(
﹣1)∪( ![]() ﹣1,1)
﹣1,1)
【解析】(1)求出函数导数,由两直线垂直斜率之积为﹣1,解方程可得b;(2)求出导数,对a讨论,①若a≤ ![]() ,则
,则 ![]() ≤1,②若
≤1,②若 ![]() <a<1,则
<a<1,则 ![]() >1,③若a>1,分别求出单调区间,可得最小值,解不等式即可得到所求范围.
>1,③若a>1,分别求出单调区间,可得最小值,解不等式即可得到所求范围.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos4x+sin2x,下列结论中错误的是( )
A.f(x)是偶函数
B.函f(x)最小值为 ![]()
C.![]() 是函f(x)的一个周期
是函f(x)的一个周期
D.函f(x)在(0, ![]() )内是减函数
)内是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:y= ![]() x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: ![]() ﹣y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
﹣y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|x﹣a|.
(1)若a≤2,解不等式f(x)≥2;
(2)若a>1,x∈R,f(x)+|x﹣1|≥1,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的部分图象如图所示.
的部分图象如图所示.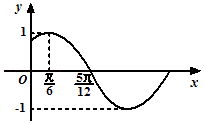
(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,若(2a﹣c)cosB=bcosC,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式: (x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
…
观察多项式系数之间的关系,可以仿照杨辉三角构造如图所示的广义杨辉三角形,其构造方法为:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(1+ax)(x2+x+1)5的展开式中,x7项的系数为75,则实数a的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,直线的参数方程为 ![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程,并指出其表示何种曲线;
(2)设直线l与曲线C交于A,B两点,若点P的直角坐标为(1,0),试求当 ![]() 时,|PA|+|PB|的值.
时,|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求函数 ![]() 在x
在x ![]() 1处的切线方程;
1处的切线方程;
(2)若存在 ![]()
![]() ,使得
,使得 ![]() 成立,其中
成立,其中 ![]() 为常数,
为常数,
求证: ![]() ;
;
(3)若对任意的 ![]() ,不等式
,不等式 ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第一组[160,164],第二组[164,168],…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图. (Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172cm以上(含172cm)的人数;
(Ⅲ)在这50名男生身高在172cm以上(含172cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为ξ,求ξ的数学期望.
参考数据:若ξ﹣N(μ,σ2),则p(μ﹣σ<ξ≤μ+σ)=0.6826,p(μ﹣2σ<ξ≤μ+2σ)=0.9544,p(μ﹣3σ<ξ≤μ+3σ)=0.9974.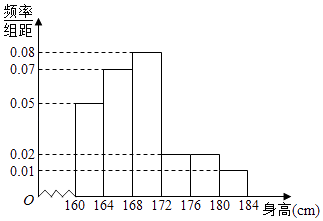
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com