
【题目】已知函数 ![]() ,
, ![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求函数 ![]() 在x
在x ![]() 1处的切线方程;
1处的切线方程;
(2)若存在 ![]()
![]() ,使得
,使得 ![]() 成立,其中
成立,其中 ![]() 为常数,
为常数,
求证: ![]() ;
;
(3)若对任意的 ![]() ,不等式
,不等式 ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】
(1)
解:(1)因为 ![]() ,所以
,所以 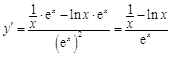 ,故
,故 ![]() .
.
所以函数 ![]() 在x
在x ![]() 1处的切线方程为
1处的切线方程为 ![]() ,
,
即 ![]() .
.
(2)
由已知等式 ![]() 得
得 ![]() .
.
记 ![]() ,则
,则 ![]() .
.
假设 ![]() .
.
①若 ![]() ,则
,则 ![]() ,所以
,所以 ![]() 在
在 ![]() 上为单调增函数.
上为单调增函数.
又 ![]() ,所以
,所以 ![]() ,与
,与 ![]() 矛盾.
矛盾.
②若 ![]() ,记
,记 ![]() ,则
,则 ![]() .
.
令 ![]() ,解得
,解得 ![]() .
.
当 ![]() 时,
时, ![]() ,
, ![]() 在
在 ![]() 上为单调增函数;
上为单调增函数;
当 ![]() 时,
时, ![]() ,
, ![]() 在
在 ![]() 上为单调减函数.
上为单调减函数.
所以 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() 在
在 ![]() 上为单调增函数.
上为单调增函数.
又 ![]() ,所以
,所以 ![]() ,与
,与 ![]() 矛盾.
矛盾.
综合①②,假设不成立,所以 ![]() .
.
(3)
由 ![]() 得
得 ![]() .
.
记 ![]() ,
, ![]() ,
,
则 ![]() .
.
①当 ![]() 时,因为
时,因为 ![]() ,
, ![]() ,所以
,所以 ![]() ,
,
所以 ![]() 在
在 ![]() 上为单调增函数,所以
上为单调增函数,所以 ![]() ,
,
故原不等式恒成立.
法一:
②当 ![]() 时,由(2)知
时,由(2)知 ![]() ,
, ![]() ,
,
当 ![]() 时,
时, ![]() ,
, ![]() 为单调减函数,
为单调减函数,
所以 ![]() ,不合题意.
,不合题意.
法二:
②当 ![]() 时,一方面
时,一方面 ![]() .
.
另一方面, ![]() ,
, ![]() .
.
所以 ![]() ,使
,使 ![]() ,又
,又 ![]() 在
在 ![]() 上为单调减函数,
上为单调减函数,
所以当 ![]() 时,
时, ![]() ,故
,故 ![]() 在
在 ![]() 上为单调减函数,
上为单调减函数,
所以 ![]() ,不合题意.
,不合题意.
综上, ![]() .
.
【解析】(1.)利用积函数的导函数法则求出导函数再将x=1代入求出斜率求出切线方程。
(2.)假设 ![]() ,将
,将 ![]() 整理为
整理为 ![]() ,求导又单调性判断是否在不同点存在相同的y值
,求导又单调性判断是否在不同点存在相同的y值
(3.)对 ![]() 求导然后分
求导然后分 ![]() 、
、 ![]() 两种情况讨论。
两种情况讨论。
【考点精析】本题主要考查了复合函数单调性的判断方法的相关知识点,需要掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”才能正确解答此题.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为D,若对于a,b,c∈D,f(a),f(b),f(c)分别为某个三角形的三边长,则称f(x)为“三角形函数”.给出下列四个函数: ①f(x)=lg(x+1)(x>0);
②f(x)=4﹣cosx;
③ ![]() ;
;
④ ![]()
其中为“三角形函数”的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+b)lnx,g(x)=alnx+ ![]() ﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
(1)求b的值;
(2)若对任意x≥1,都有g(x)> ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知a1=9,a2为整数,且Sn≤S5 .
(1)求{an}的通项公式;
(2)设数列 ![]() 的前n项和为Tn , 求证:
的前n项和为Tn , 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有1 000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数见右上表,据此估计这1 000根中纤维长度不小于37.5 mm的根数是 .
纤维长度 | 频数 |
[22.5,25.5) | 3 |
[25.5,28.5) | 8 |
[28.5,31.5) | 9 |
[31.5,34.5) | 11 |
[34.5,37.5) | 10 |
[37.5,40.5) | 5 |
[40.5,43.5] | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》之后,人们学会了用数列的知识来解决问题.公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”.利用这种思想设计的一个程序框图如图,若输出的S值为九匹三丈(一匹=4丈,一丈=10尺),则框图中d为( )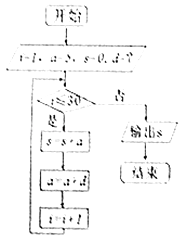
A.![]() 尺
尺![]()
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.
=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.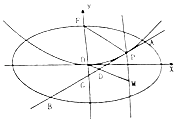
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于A,B两点且与抛物线E在第一象限相切于点P,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M,求 ![]() 的最小值及此时点P的坐标.
的最小值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() =2csinA
=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,其前n项和为Sn , 若S9=99,且a4 , a7 , a12成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com