
【题目】设等差数列{an}的前n项和为Sn , 已知a1=9,a2为整数,且Sn≤S5 .
(1)求{an}的通项公式;
(2)设数列 ![]() 的前n项和为Tn , 求证:
的前n项和为Tn , 求证: ![]() .
.
【答案】
(1)解:a1=9,a2为整数,可知:等差数列{an}的公差d为整数,
由Sn≤S5,∴a5≥0,a6≤0,则9+4d≥0,9+5d≤0,解得 ![]() ,d为整数,d=﹣2.
,d为整数,d=﹣2.
∴an=9﹣2(n﹣1)=11﹣2n
(2)证明: ![]() =
= ![]() =
= ![]() .
.
∴数列 ![]() 的前n项和Tn=
的前n项和Tn= ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() .
.
令bn= ![]() ,由于函数f(x)=
,由于函数f(x)= ![]() 的图象关于点(4.5,0)对称及其单调性,可知:0<b1<b2<b3<b4,b5<b6<b7<…<0,∴bn≤b4=1.∴
的图象关于点(4.5,0)对称及其单调性,可知:0<b1<b2<b3<b4,b5<b6<b7<…<0,∴bn≤b4=1.∴ ![]() =
= ![]()
【解析】(1)a1=9,a2为整数,可知:等差数列{an}的公差d为整数,由Sn≤S5 , 可得a5≥,a6≤0,可得d=﹣2.即可得出.(2) ![]() =
= ![]() =
= ![]() .利用“裂项求和”方法与数列的单调性即可得出.
.利用“裂项求和”方法与数列的单调性即可得出.
【考点精析】关于本题考查的数列的前n项和,需要了解数列{an}的前n项和sn与通项an的关系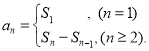 才能得出正确答案.
才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|x﹣a|.
(1)若a≤2,解不等式f(x)≥2;
(2)若a>1,x∈R,f(x)+|x﹣1|≥1,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式: (x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
…
观察多项式系数之间的关系,可以仿照杨辉三角构造如图所示的广义杨辉三角形,其构造方法为:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(1+ax)(x2+x+1)5的展开式中,x7项的系数为75,则实数a的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,直线的参数方程为 ![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程,并指出其表示何种曲线;
(2)设直线l与曲线C交于A,B两点,若点P的直角坐标为(1,0),试求当 ![]() 时,|PA|+|PB|的值.
时,|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C的参数方程为 ![]() (t为参数,a>0)以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知直线l的极坐标方程为
(t为参数,a>0)以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知直线l的极坐标方程为 ![]() .
.
(Ⅰ)设P是曲线C上的一个动点,当a=2时,求点P到直线l的距离的最小值;
(Ⅱ)若曲线C上的所有点均在直线l的右下方,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求函数 ![]() 在x
在x ![]() 1处的切线方程;
1处的切线方程;
(2)若存在 ![]()
![]() ,使得
,使得 ![]() 成立,其中
成立,其中 ![]() 为常数,
为常数,
求证: ![]() ;
;
(3)若对任意的 ![]() ,不等式
,不等式 ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若曲线C1:x2+y2﹣4x=0与曲线C2:y(y﹣mx﹣x)=0有四个不同的交点,则实数m的取值范围是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,0)∪(0,
,0)∪(0, ![]() )
)
C.[﹣ ![]() ,
, ![]() ]
]
D.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为 . (参考数据:sin15°=0.2588,sin7.5°=0.1305) 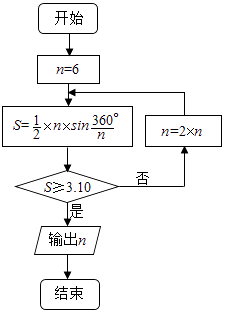
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com