
【题目】将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式: (x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
…
观察多项式系数之间的关系,可以仿照杨辉三角构造如图所示的广义杨辉三角形,其构造方法为:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(1+ax)(x2+x+1)5的展开式中,x7项的系数为75,则实数a的值为 . 
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2﹣xlna(a>0,a≠1).
(Ⅰ)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(Ⅱ)若函数y=|f(x)﹣t|﹣1有三个零点,求t的值;
(Ⅲ)若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+b)lnx,g(x)=alnx+ ![]() ﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
(1)求b的值;
(2)若对任意x≥1,都有g(x)> ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的一个焦点为F(3,0),其左顶点A在圆O:x2+y2=12上.
的一个焦点为F(3,0),其左顶点A在圆O:x2+y2=12上.
(1)求椭圆C的方程;
(2)直线l:x=my+3(m≠0)交椭圆C于M,N两点,设点N关于x轴的对称点为N1(点N1与点M不重合),且直线N1M与x轴的交于点P,试问△PMN的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知a1=9,a2为整数,且Sn≤S5 .
(1)求{an}的通项公式;
(2)设数列 ![]() 的前n项和为Tn , 求证:
的前n项和为Tn , 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》之后,人们学会了用数列的知识来解决问题.公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”.利用这种思想设计的一个程序框图如图,若输出的S值为九匹三丈(一匹=4丈,一丈=10尺),则框图中d为( )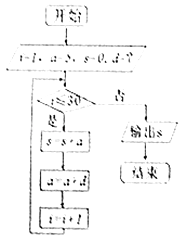
A.![]() 尺
尺![]()
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果.《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、…、《辑古算经》等算经10部专著,有着十分丰富多彩的内容,是了解我国古代数学的重要文献.这10部专著中有7部产生于魏晋南北朝时期.某中学拟从这10部名著中选择2部作为“数学文化”校本课程学习内容,则所选2部名著中至少有一部是魏晋南北朝时期的名著的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com