练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在等腰直角△ABC中，AC=BC，D在AB边上且满足： ，若∠ACD=60°，则t的值为（ ）
    A.
    B.
    C.
    D.

    【答案】A
    【解析】解：∵ ， ∴A，B，D三点共线，
    ∴由题意建立如图所示坐标系，

    设AC=BC=1，
    则C（0，0），A（1，0），B（0，1），
    直线AB的方程为x+y=1，
    直线CD的方程为y= x，
    故联立解得，x= ，y= ，
    故D（ ， ），
    故 =（ ， ）， =（1，0）， =（0，1），
    故t +（1﹣t） =（t，1﹣t），
    故（ ， ）=（t，1﹣t），
    故t= ，
    故选：A．
    【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识，掌握如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在△ABC内角A，B，C的对边分别是a，b，c，cos = ，且acosB+bcosA=2，则△ABC的面积的最大值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2011年，国际数学协会正式宣布，将每年的3月14日设为国际数学节，来源是中国古代数学家祖冲之的圆周率．为庆祝该节日，某校举办的数学嘉年华活动中，设计了一个有奖闯关游戏，游戏分为两个环节． 第一环节“解锁”：给定6个密码，只有一个正确，参赛选手从6个密码中任选一个输入，每人最多可输三次，若密码正确，则解锁成功，该选手进入第二个环节，否则直接淘汰．
    第二环节“闯关”：参赛选手按第一关、第二关、第三关的顺序依次闯关，若闯关成功，分别获得10个、20个、30个学豆的奖励，游戏还规定，当选手闯过一关后，可以选择带走相应的学豆，结束游戏，也可以选择继续闯下一关，若有任何一关没有闯关成功，则全部学豆归零，游戏结束．设选手甲能闯过第一关、第二关、第三关的概率分别为 ，选手选择继续闯关的概率均为 ，且各关之间闯关成功与否互不影响．
    （1）求某参赛选手能进入第二环节的概率；
    （2）设选手甲在第二环节中所得学豆总数为X，求X的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数F（x）=xf（x），f（x）满足f（x）=f（﹣x），且当x∈（﹣∞，0]时，F'（x）＜0成立，若 ，则a，b，c的大小关系是（ ）
    A.a＞b＞c
    B.c＞a＞b
    C.c＞b＞a
    D.a＞c＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣1|+|x﹣a|．
    （1）若a≤2，解不等式f（x）≥2；
    （2）若a＞1，x∈R，f（x）+|x﹣1|≥1，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，且∠ABC=120°．点E是棱PC的中点，平面ABE与棱PD交于点F． （Ⅰ）求证：AB∥EF；
    （Ⅱ）若PA=PD=AD=2，且平面PAD⊥平面ABCD，求平面PAF与平面AEF所成的二面角的正弦值．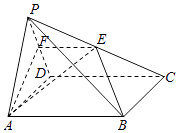

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将三项式（x2+x+1）n展开，当n=0，1，2，3，…时，得到以下等式： （x2+x+1）0=1
    （x2+x+1）1=x2+x+1
    （x2+x+1）2=x4+2x3+3x2+2x+1
    （x2+x+1）3=x6+3x5+6x4+7x3+6x2+3x+1
    …
    观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数（不足3数的，缺少的数计为0）之和，第k行共有2k+1个数．若在（1+ax）（x2+x+1）5的展开式中，x7项的系数为75，则实数a的值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xoy中，曲线C的参数方程为 （t为参数，a＞0）以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，已知直线l的极坐标方程为 ．
    （Ⅰ）设P是曲线C上的一个动点，当a=2时，求点P到直线l的距离的最小值；
    （Ⅱ）若曲线C上的所有点均在直线l的右下方，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以原点为极点，x轴为极轴建立极坐标系，曲线C1的方程为 （θ为参数），曲线C2的极坐标方程为C2：ρcosθ+ρsinθ=1，若曲线C1与C2相交于A、B两点．
    （1）求|AB|的值；
    （2）求点M（﹣1，2）到A、B两点的距离之积．

    查看答案和解析>>

    同步练习册答案