
【题目】斜率为 ![]() 的直线l与椭圆
的直线l与椭圆 ![]() +
+ ![]() =1(a>b>0)交于不同的两点A、B.若点A、B在x轴上的射影恰好为椭圆的两个焦点.
=1(a>b>0)交于不同的两点A、B.若点A、B在x轴上的射影恰好为椭圆的两个焦点.
(1)求椭圆的离心率;
(2)P是椭圆上的动点,若△PAB面积最大值是4 ![]() ,求该椭圆的方程.
,求该椭圆的方程.
【答案】
(1)解:由题意知:直线与椭圆两交点的横坐标为﹣c,c,纵坐标分别为﹣ ![]() ,
, ![]() ,
,
∴由 ![]() =
= ![]()
转化为:2b2=2(a2﹣c2)= ![]() ac
ac
即2e2+ ![]() e﹣2=0,
e﹣2=0,
解得e= ![]() ,e=﹣
,e=﹣ ![]() (负根舍去),
(负根舍去),
∴椭圆的离心率为e= ![]() ;
;
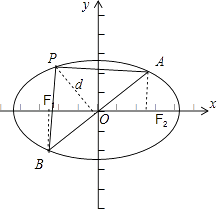
(2)解:∵P是椭圆上的动点,当△PAB的面积最大值是4 ![]() 时,
时,
有 ![]() |AB|h=4
|AB|h=4 ![]() ,
,
∵e= ![]() ,∴b=c,
,∴b=c,
∴a= ![]() c;
c;
∴设椭圆的方程为 ![]() +
+ ![]() =1,
=1,
则|AB|= ![]() c,
c,
∴三角形PAB的高为h= ![]() ;
;
又直线为y= ![]() x,
x,
即 ![]() x﹣2y=0;
x﹣2y=0;
则点P( ![]() ccosθ,csinθ)到直线的距离表示为
ccosθ,csinθ)到直线的距离表示为
d= ![]() =
= ![]() ≤
≤ ![]() ,
,
令 ![]() =
= ![]() ,
,
解得c=2,
∴椭圆的方程为 ![]() +
+ ![]() =1.
=1.
【解析】(1)画出图形,结合图形,得出直线与椭圆两交点坐标,根据两点间的斜率公式,求出离心率e;(2)由(1)知,设出椭圆的标准方程 ![]() +
+ ![]() =1,求出|AB|的值,利用三角形的面积求出高h;再求点P到直线的最大距离d,由此求出c即可.
=1,求出|AB|的值,利用三角形的面积求出高h;再求点P到直线的最大距离d,由此求出c即可.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() ⊥
⊥ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |=t,若P点是△ABC所在平面内一点,且
|=t,若P点是△ABC所在平面内一点,且 ![]() =
= ![]() +
+ ![]() ,当t变化时,
,当t变化时, ![]() 的最大值等于( )
的最大值等于( )
A.﹣2
B.0
C.2
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1、F2是双曲线C: ![]() =1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )
=1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )
A.(1,+∞)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.(1, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为
=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为 ![]() ,则p=( )
,则p=( )
A.1
B.![]()
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P( ![]() ,1)和椭圆C:
,1)和椭圆C: ![]() +
+ ![]() =1.
=1.
(1)设椭圆的两个焦点分别为F1 , F2 , 试求△PF1F2的周长及椭圆的离心率;
(2)若直线l: ![]() x﹣2y+m=0(m≠0)与椭圆C交于两个不同的点A,B,设直线PA与PB的斜率分别为k1 , k2 , 求证:k1+k2=0.
x﹣2y+m=0(m≠0)与椭圆C交于两个不同的点A,B,设直线PA与PB的斜率分别为k1 , k2 , 求证:k1+k2=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 经过点M(﹣2,﹣1),离心率为
经过点M(﹣2,﹣1),离心率为 ![]() .过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q. (I)求椭圆C的方程;
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q. (I)求椭圆C的方程;
(II)试判断直线PQ的斜率是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图程序框图的算法思路,源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法,执行该程序框图,若输入的n,an , x分别为5,1,﹣2,且a4=5,a3=10,a2=10,a1=5,a0=1,则输出的v=( ) 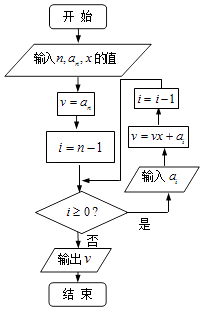
A.1
B.2
C.﹣1
D.﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C 的参数方程为 ![]() (α为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C 的极坐标方程;
(α为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C 的极坐标方程;
(Ⅱ)设l1:θ= ![]() ,l2:θ=
,l2:θ= ![]() ,若l 1、l2与曲线C 相交于异于原点的两点 A、B,求△AOB的面积.
,若l 1、l2与曲线C 相交于异于原点的两点 A、B,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com